题目内容
已知函数f(x)=sin(
-2x)-2sin2x+1(x∈R),
(1)求函数f(x)的周期及单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知函数f(x)的图象经过点(A,
),b,a,c成等差数列,且
•
=9,求a的值.
| 7π |
| 6 |
(1)求函数f(x)的周期及单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知函数f(x)的图象经过点(A,
| 1 |
| 2 |
| AB |
| AC |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,三角函数的周期性及其求法
专题:三角函数的图像与性质,解三角形
分析:(1)利用两角和与差的三角函数以及二倍角公式化简函数为一个角的一个三角函数的形式,通过周期公式求函数f(x)的周期,利用正弦函数的单调增区间求解函数的单调递增区间;
(2)通过函数f(x)的图象经过点(A,
),b,a,c成等差数列,求出A以及列出abc的关系,利用
•
=9,求出bc的值,通过余弦定理求a的值.
(2)通过函数f(x)的图象经过点(A,
| 1 |
| 2 |
| AB |
| AC |
解答:
解:f(x)=sin(
-2x)-2sin2x+1=-
cos2x+
sin2x+cos2x=
cos2x+
sin2x=sin(2x+
)…(3分)
(1)最小正周期:T=
=π,…(4分)
由2kπ-
≤2x+
≤2kπ+
(k∈Z)可解得:kπ-
≤x≤kπ+
(k∈Z),
所以f(x)的单调递增区间为:[kπ-
,kπ+
](k∈Z); …(6分)
(2)由f(A)=sin(2A+
)=
可得:2A+
=
+2kπ或
+2kπ(k∈Z)
∴A=
,…(8分)
又∵b,a,c成等差数列,
∴2a=b+c,…(9分)
而
•
=bccosA=
bc=9,
∴bc=18 …(10分)
∴cosA=
=
-1=
-1=
-1,
∴a=3
.…(12分)
| 7π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
(1)最小正周期:T=
| 2π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
所以f(x)的单调递增区间为:[kπ-
| π |
| 3 |
| π |
| 6 |
(2)由f(A)=sin(2A+
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴A=
| π |
| 3 |
又∵b,a,c成等差数列,
∴2a=b+c,…(9分)
而
| AB |
| AC |
| 1 |
| 2 |
∴bc=18 …(10分)
∴cosA=
| 1 |
| 2 |
| (b+c)2-a2 |
| 2bc |
| 4a2-a2 |
| 36 |
| a2 |
| 12 |
∴a=3
| 2 |
点评:本题考查三角形的解法,两角和与差的三角函数以及二倍角公式的应用,三角函数的图象与性质,基本知识的考查.

练习册系列答案
相关题目
数列{an}的通项公式为an=2n+4n-2,则数列{an}的前n项和sn=( )
| A、2n+2n2-1 |
| B、2n+2n2-2 |
| C、2n+1+2n2-1 |
| D、2n+1+2n2-2 |
过双曲线
-
=1(a>0,b>0)的一个焦点作实轴的垂线,交双曲线于A,B两点,若线段AB的长度恰等于焦距,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知变量x,y满足约束条件
,则z=4x+y的最小值为( )
|
| A、55 | B、-55 | C、5 | D、-5 |
已知集合A={x||2x+1|>3},集合B={x|y=
},则A∩(∁RB)=( )
|
| A、(1,2) |
| B、(1,2] |
| C、(1,+∞) |
| D、[1,2] |
 某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.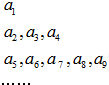 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.