题目内容
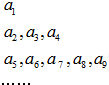 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)若图中从第2行开始,每一行中的数按从左到右的顺序均成等比数列,且公比是同一个正数,已知a19=
| 5 |
| 2 |
考点:数列的应用,数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)设{bn}的公差为d,利用b2=4,b5=10,建立方程组,由此能求出数列{bn}的通项公式.
(2)设每一行组成的等比数列的公比为q,由于前n行共有1+3+5+…+(2n-1)=n2个数,且42<19<52,解得q=
,cn=
,由错位相减法能够求得Sn.
(2)设每一行组成的等比数列的公比为q,由于前n行共有1+3+5+…+(2n-1)=n2个数,且42<19<52,解得q=
| 1 |
| 2 |
| n |
| 2n-2 |
解答:
解:(Ⅰ)设{bn}的公差为d,
则
,解得
,∴bn=2n.
(Ⅱ)设每一行组成的等比数列的公比为q,
由于前n行共有1+3+5+…+(2n-1)=n2个数,且42<19<52,
∴a17=b5=10,
∴a19=a17q2=10q2,
又a19=
,解得q=
,
∴cn=
,
∴Sn=c1+c2+…+cn=
+
+…+
,
∴
Sn=
+
+…+
,
两式相减可得
Sn=4-
,
∴Sn=8-
.
则
|
|
(Ⅱ)设每一行组成的等比数列的公比为q,
由于前n行共有1+3+5+…+(2n-1)=n2个数,且42<19<52,
∴a17=b5=10,
∴a19=a17q2=10q2,
又a19=
| 5 |
| 2 |
| 1 |
| 2 |
∴cn=
| n |
| 2n-2 |
∴Sn=c1+c2+…+cn=
| 1 |
| 2-1 |
| 2 |
| 20 |
| n |
| 2n-2 |
∴
| 1 |
| 2 |
| 1 |
| 20 |
| 2 |
| 21 |
| n |
| 2n-1 |
两式相减可得
| 1 |
| 2 |
| n+2 |
| 2n-1 |
∴Sn=8-
| n+2 |
| 2n-2 |
点评:本题考查数列的通项公式的求法、前n项和的计算和等比数列性质的应用,解题时要注意方程思想和错位相减求和法的合理运用,注意合理地进行等价转化.

练习册系列答案
相关题目