题目内容
数列{an}的通项公式为an=2n+4n-2，则数列{an}的前n项和sn=（ ）
| A、2n+2n2-1 |
| B、2n+2n2-2 |
| C、2n+1+2n2-1 |
| D、2n+1+2n2-2 |
考点：数列的求和
专题：等差数列与等比数列
分析：由an=2n+4n-2，利用分组求和法能求出数列{an}的前n项和Sn．
解答：
解：∵an=2n+4n-2，
∴Sn=（2+22+23+…+2n）+4（1+2+3+…+n）-2n
=
+4×
-2n
=2n+1-2+2n2+2n-2n
=2n+1+2n2-2．
故选：D．
∴Sn=（2+22+23+…+2n）+4（1+2+3+…+n）-2n
=
| 2(1-2n) |
| 1-2 |
| n(n+1) |
| 2 |
=2n+1-2+2n2+2n-2n
=2n+1+2n2-2．
故选：D．
点评：本题考查数列的前n项和的求法，是基础题，解题时要认真审题，注意分组求和法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
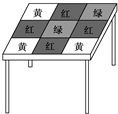一张方桌的图案如图所示，将一颗豆子随机地扔到桌面上，假设豆子不落在线上，下列事件的概率（1）豆子落在红色区域概率为
| 4 |
| 9 |
（2）豆子落在黄色区域概率为
| 1 |
| 3 |
（3）豆子落在绿色区域概率为
| 2 |
| 9 |
（4）豆子落在红色或绿色区域概率为
| 1 |
| 3 |
（5）豆子落在黄色或绿色区域概率为
| 4 |
| 9 |
其中正确的结论有（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
已知数列{an}是等差数列，a1=tan225°，a5=13a1，设Sn为数列{（-1）nan}的前n项和，则S2014=（ ）
| A、2014 | B、-2014 |
| C、3021 | D、-3021 |