题目内容

已知函数f（x）=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜
π
2
)的图象在y轴上的截距为1，它在y轴右侧的第一个最大值点和最小值点分别为（x0，2）和（x0+π，-2）．
（1）求f（x）的解析式；
（2）若?m∈R，?x∈[-
π
3
，
π
3
]，使f(x)≤
m
2
 
-3m-2成立，求m的取值范围．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换
专题：计算题,三角函数的图像与性质
分析：（1）由已知中函数图象在y轴右侧的第一个最大值点和最小值点分别为（x0，2）和（x0+π，-2）．易求出函数的最值及周期，进而求出A，ω值，再由图象在y轴上的截距为1，|ϕ|＜
π
2
，将（0，1）点代入可求出φ值，即可得到f（x）的解析式；
（2）通过x 的范围求出函数的最大值，然后求解不等式的解集即可．
解答： 解：（1）∵函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的图象
在y轴右侧的第一个最大值点和最小值点分别为（x0，2）和（x0+π，-2）．
∴T=2π，即ω=1，A=2，
∴f（x）=2sin（x+ϕ），
又∵函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|ϕ|＜
π
2
）的图象在y轴上的截距为1，
∴函数图象过（0，1），
∴sinϕ=
1
2
，
∵|ϕ|＜
π
2
，
∴ϕ=
π
6
，
∴f（x）=2sin（x+
π
6
）；
（2）f（x）=2sin（x+
π
6
）在x∈[-
π
3
，
π
3
]时函数的最大值为：2．
∴2≤
m
2
 
-3m-2，
解得：m≥1或m≤-1．
点评：本题考查的知识点是函数y=Asin（ωx+φ）的图象变换，函数y=Asin（ωx+φ）的解析式的求法，其中根据已知求出函数的最值，周期，向左平移量，特殊点等，进而求出A，ω，φ值，得到函数的解析式是解答本题的关键．
练习册系列答案
相关题目
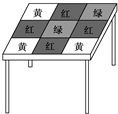一张方桌的图案如图所示，将一颗豆子随机地扔到桌面上，假设豆子不落在线上，下列事件的概率
（1）豆子落在红色区域概率为
4
9
；
（2）豆子落在黄色区域概率为
1
3
；
（3）豆子落在绿色区域概率为
2
9
；
（4）豆子落在红色或绿色区域概率为
1
3
；     
（5）豆子落在黄色或绿色区域概率为
4
9
．
其中正确的结论有（　　）
A、2个B、3个C、4个D、5个
双曲线2x2-y2=-1的离心率为（　　）
A、
6
2
B、
3
C、
2
D、
2
2
若z=
2-i
1+2i
，则复数z的虚部为（　　）
A、iB、-iC、1D、-1
已知函数f(x)=sin(
7π
6
-2x)-2sin2x+1(x∈R)，
（1）求函数f（x）的周期及单调递增区间；
（2）在△ABC中，三内角A，B，C的对边分别为a，b，c，已知函数f（x）的图象经过点(A，
1
2
)，b，a，c成等差数列，且
AB
•
AC
=9，求a的值．
设函数f（x）=sinx+sin（x+
π
3
）．
（1）求f（x）的最小值，并求使f（x）取得最小值的x的集合；
（2）在△ABC中，设角A，B的对边分别为a，b，若B=2A，且b=2af（A-
π
6
），求角C的大小．
已知函数f（x）=x4+x2-1，g（x）=ax3+x2+b（x∈R），其中a，b∈R．
（Ⅰ）若曲线y=f（x）与y=g（x）在点（1，1）处相交且有相同的切线，求a，b的值；
（Ⅱ）设F（x）=f（x）+g（x），若对于任意的a∈[-2，2]，函数y=F（x）在区间[-1，1]上的值恒为负数，求b的取值范围．
在数列{an}中，a2n=qn，a2n-1=d(n+1)，(n∈N*)，且前n项和为Sn，若a5=S2=8．
（1）求实数q，d；      
（2）求数列{an}的前n项和为Sn．
已知F1，F2是双曲线E的两个焦点，以线段F1F2为直径的圆与双曲线的一个公共点是M，若∠MF1F2=30°，则双曲线E的离心率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网