题目内容
设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是 (填序号).
①若AC与BD共面,则AD与BC共面;
②若AC与BD是异面直线,则AD与BC是异面直线;
③AB=AC,DB=DC,则AD=BC;
④AB=AC,DB=DC,则AD⊥BC.
①若AC与BD共面,则AD与BC共面;
②若AC与BD是异面直线,则AD与BC是异面直线;
③AB=AC,DB=DC,则AD=BC;
④AB=AC,DB=DC,则AD⊥BC.
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①当AC与BD共面时,证明AD与BC也共面;
②用反证法证明AD与BC是异面直线;
③④画出图形,可以判定AD与BC不一定相等,证明BC与AD一定垂直.
②用反证法证明AD与BC是异面直线;
③④画出图形,可以判定AD与BC不一定相等,证明BC与AD一定垂直.
解答:
解:①当AC与BD共面时,不妨设AC与BD确定平面α,∵AC?α,BD?α,∴A∈α,D∈α,∴AD?α,同理BC?α,∴AD与BC共面,命题正确;
②假设AD与BC共面,由①知,AC与BD也共面,这与AC与BD是异面直线矛盾,∴假设不成立,∴AD与BC是异面直线,∴命题正确;
③如图,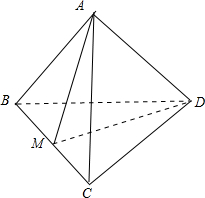 空间四边形ABCD中,AB=AC,DB=DC,则AD与BC不一定相等,∴命题错误;
空间四边形ABCD中,AB=AC,DB=DC,则AD与BC不一定相等,∴命题错误;
④如③中图,取BC的中点M,连接AM、DM,AM⊥BC,DM⊥BC,∴BC⊥平面ADM,∴BC⊥AD,∴命题正确;
∴正确的命题是①②④,不正确的是③;
故答案为:③.
②假设AD与BC共面,由①知,AC与BD也共面,这与AC与BD是异面直线矛盾,∴假设不成立,∴AD与BC是异面直线,∴命题正确;
③如图,
 空间四边形ABCD中,AB=AC,DB=DC,则AD与BC不一定相等,∴命题错误;
空间四边形ABCD中,AB=AC,DB=DC,则AD与BC不一定相等,∴命题错误;④如③中图,取BC的中点M,连接AM、DM,AM⊥BC,DM⊥BC,∴BC⊥平面ADM,∴BC⊥AD,∴命题正确;
∴正确的命题是①②④,不正确的是③;
故答案为:③.
点评:本题通过命题真假的判定,考查了空间中的直线共面与异面以及垂直问题,是综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题中的真命题是( )
A、?x∈R,使得sinxcosx=
| ||
| B、?x∈(-∞,0),2x>1 | ||
| C、?x∈R,x2≥x-1 | ||
| D、?x∈(0,π),sinx>cosx |