题目内容
已知f(x)=x2+1,对任意x∈(0,+∞),f(
)-2m2f(x)≤f(x-2)-2f(m)恒成立,则实数m的取值范围是( )
| x |
| m |
A、(-∞,-
| ||||||||
B、(-∞,-
| ||||||||
C、(-∞,-1]∪[
| ||||||||
| D、(-∞,-1]∪[1,+∞) |
考点:函数恒成立问题,二次函数的性质
专题:综合题,函数的性质及应用,不等式的解法及应用
分析:分离参数m后,圆不等式可化为
-2m2≤1-
+
,则问题转化为
-2m2≤(1-
+
)min,利用导数可求最小值.
| 1 |
| m2 |
| 4 |
| x |
| 2 |
| x2 |
| 1 |
| m2 |
| 4 |
| x |
| 2 |
| x2 |
解答:
解:f(
)-2m2f(x)≤f(x-2)-2f(m),即(
)2+1-2m2(x2+1)≤(x-2)2+1-2(m2+1),
整理得(
-2m2)x2≤x2-4x+2,
∵x∈(0,+∞),
∴
-2m2≤1-
+
,
令g(x)=1-
+
(x>0),
则g′(x)=
-
=
,
当0<x<1时,g′(x)<0,g(x)递减;当x>1时,g′(x)>0,g(x)递增.
∴x=1时,g(x)取得极小值,也为最小值,是g(1)=-1,
∴
-2m2≤-1,解得m≤-1或m≥1,
故选D.
| x |
| m |
| x |
| m |
整理得(
| 1 |
| m2 |
∵x∈(0,+∞),
∴
| 1 |
| m2 |
| 4 |
| x |
| 2 |
| x2 |
令g(x)=1-
| 4 |
| x |
| 2 |
| x2 |
则g′(x)=
| 4 |
| x2 |
| 4 |
| x3 |
| 4(x-1) |
| x3 |
当0<x<1时,g′(x)<0,g(x)递减;当x>1时,g′(x)>0,g(x)递增.
∴x=1时,g(x)取得极小值,也为最小值,是g(1)=-1,
∴
| 1 |
| m2 |
故选D.
点评:该题考查函数恒成立、二次函数的性质,考查利用导数求函数的最值,考查转化思想,直接求函数最值或分离参数后求函数最值是解决恒成立问题的基本思路.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
从集合A={1,2,3,4,5}任意取出两个数,这两个数的和是偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设随机变量ξ~N(3,σ2),若P(ξ≥7)=0.16,则P(-1≤ξ≤7)=( )
| A、0.84 | B、0.68 |
| C、0.32 | D、0.16 |
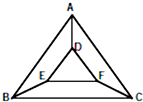 如图,用四种不同颜色给图中的ABCDEF六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,而且四种不同颜色要全部用完,则不同的涂色方法共有( )种.
如图,用四种不同颜色给图中的ABCDEF六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,而且四种不同颜色要全部用完,则不同的涂色方法共有( )种.| A、144 | B、216 |
| C、264 | D、360 |
从数字0,1,2,3,…,9中,按由小到大的顺序取出a1,a2,a3,且a2-a1≥2,a3-a2≥2,则不同的取法有( )
| A、20种 | B、35种 |
| C、56种 | D、60种 |
已知条件p:函数f(x)=ax-2b+2 对于任意的x∈[-1,1]恒有f(x)≥0,若对任意的一个实数a∈[-2,2],一个实数 b∈[0,2],则满足条件P的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知二元函数f(x,θ)=
(x∈R,θ∈R),则f(x,θ)的最大值和最小值分别为( )
| xcosθ |
| x2+xsinθ+2 |
A、
| ||||||||
B、
| ||||||||
C、2
| ||||||||
D、2
|