题目内容

设随机变量ξ～N（3，σ2），若P（ξ≥7）=0.16，则P（-1≤ξ≤7）=（　　）
A、0.84B、0.68
C、0.32D、0.16
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：利用ξ～N（3，σ2），可得图象关于x=3对称，结合P（ξ≥7）=0.16，即可求得结论．
解答： 解：∵ξ～N（3，σ2），∴图象关于x=3对称
∵P（ξ≥7）=0.16，
∴P（-1≤ξ≤7）=1-0.16×2=0.68．
故选：B．
点评：本题考查正态分布曲线的对称性，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
若实数a，b满足log2（a-2）+log2（2b-2）=3，则a+b的最小值是
 
．
如图，设G、H分别为△ABC的重心、垂心，F为线段GH的中点，若△ABC外接圆的半径为1，则|
AF
|2+|
BF
|2+|
CF
|2=
 
．
在△ABC中，角A，B，C的对边分别为a，b，c，AH为BC边上的高，给出以下四个结论：
①
AH
•
BC
=0；
②
AH
•（
AB
+
BC
）=
AH
•
AB
；
③若
AB
•
AC
＞0，则△ABC为锐角三角形；
④
AC
•
AH
|
AH
|
=csinB．
其中所有正确结论的序号是
 
．
已知复数z满足（z-1）（1+2i）=2i（i为虚数单位），则z的虚部是（　　）
A、
2
5
i
B、
2
5
C、
3
5
D、
9
5
已知f（x）=x2+1，对任意x∈（0，+∞），f（
x
m
）-2m2f（x）≤f（x-2）-2f（m）恒成立，则实数m的取值范围是（　　）
A、（-∞，-
2
2
]∪[1，+∞）
B、（-∞，-
2
2
]∪[
2
2
，+∞）
C、（-∞，-1]∪[
2
2
，+∞）
D、（-∞，-1]∪[1，+∞）
已知全集U=R，集合A={x|
x
1-x
＜0|，B={x|lgx≥0}，则集合{x|x≤1}等于（　　）
A、A∩B
B、A∪B
C、∁U（A∩B）
D、∁U（A∩B）
已知定义在R上的函数y=f（x）满足f（x+2）=f（x），当-1＜x≤1 时，f（x）=x3 则函数y=f（x）+log
1
5
|x|的零点的个数（　　）
A、3B、4C、5D、6
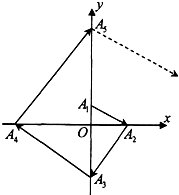如图所示，点列{An}满足：|
OA1
|=1，|
OAi+1
|=2|
OAi
|+1，Ai均在坐标轴上（i∈N*），则向量
OA1
+
OA2
+…+
OA2014
=（　　）
A、（22014-1，0）
B、（22016-1，22015-1）
C、（
22014-1
5
，
3(22014-1)
5
）
D、（
22016-1
5
，
22015-3
5
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网