题目内容
已知二元函数f(x,θ)=
(x∈R,θ∈R),则f(x,θ)的最大值和最小值分别为( )
| xcosθ |
| x2+xsinθ+2 |
A、
| ||||||||
B、
| ||||||||
C、2
| ||||||||
D、2
|
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:当x=0时,f(x,θ)=
=0,函数不取最值,当x≠0时,f(x,θ)=
,令u=x+
,则f=
,其意义为平面上单位圆上动点(cosθ,sinθ)与(-u,0)点连线斜率k的倒数,数形结合后,可得f(x,θ)的最大值和最小值.
| xcosθ |
| x2+xsinθ+2 |
| cosθ | ||
x+
|
| 2 |
| x |
| cosθ |
| sinθ+u |
解答:
解:当x=0时,f(x,θ)=
=0,
当x≠0时,f(x,θ)=
=
,
令u=x+
,则|u|≥2
,即u≤-2
,或u≥2
,
则f=
,其意义为平面上单位圆上动点(cosθ,sinθ)与(-u,0)点连线斜率k的倒数,
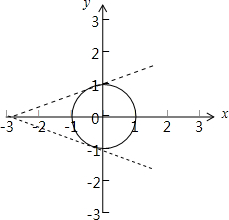
∵k∈(-∞,-
]∪[
,+∞),
故f=
∈[-
,
]
故f(x,θ)的最大值和最小值分别为
,-
,
故选:A
| xcosθ |
| x2+xsinθ+2 |
当x≠0时,f(x,θ)=
| xcosθ |
| x2+xsinθ+2 |
| cosθ | ||
x+
|
令u=x+
| 2 |
| x |
| 2 |
| 2 |
| 2 |
则f=
| cosθ |
| sinθ+u |

∵k∈(-∞,-
| 7 |
| 7 |
故f=
| cosθ |
| sinθ+u |
| ||
| 7 |
| ||
| 7 |
故f(x,θ)的最大值和最小值分别为
| ||
| 7 |
| ||
| 7 |
故选:A
点评:本题考查的知识点是函数的最值及其几何意义,其中分析出f=
,其意义为平面上单位圆上动点(cosθ,sinθ)与(-u,0)点连线斜率k的倒数,是解答的关键.
| cosθ |
| sinθ+u |

练习册系列答案
相关题目
已知f(x)=x2+1,对任意x∈(0,+∞),f(
)-2m2f(x)≤f(x-2)-2f(m)恒成立,则实数m的取值范围是( )
| x |
| m |
A、(-∞,-
| ||||||||
B、(-∞,-
| ||||||||
C、(-∞,-1]∪[
| ||||||||
| D、(-∞,-1]∪[1,+∞) |
已知△ABC中,|
|=2,A=
,则|
+
|有( )
| BC |
| π |
| 3 |
| AB |
| AC |
A、最大值
| ||
B、最大值2
| ||
C、最小值
| ||
D、最小值2
|
对于命题p:若|
|=|
|=2,
与
的夹角是
,则向量
在
方向上的投影是1;命题q:“x≤1”是“
≥1”的必要不充分条件,下列判断正确的是( )
| a |
| b |
| a |
| b |
| 2π |
| 3 |
| b |
| a |
| 1 |
| x |
| A、¬q为假命题 |
| B、¬p为假命题 |
| C、“p∧q”是真命题 |
| D、“p∨q”是假命题 |
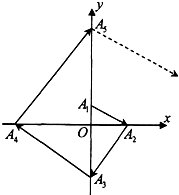 如图所示,点列{An}满足:|
如图所示,点列{An}满足:|| OA1 |
| OAi+1 |
| OAi |
| OA1 |
| OA2 |
| OA2014 |
| A、(22014-1,0) | ||||
| B、(22016-1,22015-1) | ||||
C、(
| ||||
D、(
|
两位工人加工同一种零件共100个,甲加工了40个,其中35个是合格品,乙加工了60个,其中有50个合格,令A事件为”从100个产品中任意取一个,取出的是合格品”,B事件为”从100个产品中任意取一个,取到甲生产的产品”,则P(A|B)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的部分图象如图所示,则满足a,b关系是( )
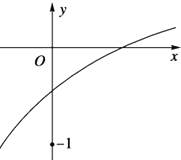

A、0<
| ||||
B、0<b<
| ||||
C、0<
| ||||
D、0<
|