题目内容
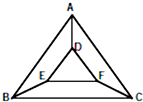如图，用四种不同颜色给图中的ABCDEF六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，而且四种不同颜色要全部用完，则不同的涂色方法共有（ ）种．| A、144 | B、216 |
| C、264 | D、360 |
考点：计数原理的应用
专题：应用题,排列组合
分析：由题意，4种颜色都用到，先给A、B、C三点涂色，再给D、E、F涂色，由乘法原理得结论．
解答：
解：由题意，4种颜色都用到，先给A、B、C三点涂色，有
种涂法，再给D、E、F涂色，因为D．E．F中必有一点用到第4种颜色
，所以另外两点用到A．B．C三点所用颜色中的两种
，此时涂法确定，
由乘法原理得
=216种．
故选：B．
| A | 3 4 |
| C | 1 3 |
| C | 2 3 |
由乘法原理得
| A | 3 4 |
| C | 1 3 |
| C | 2 3 |
故选：B．
点评：本题主要考查排列组合的基础知识，正确分步是关键，属于中档题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
设全集U=R，集合A={x|x2-2x＜0}，集合B={x|y=lg（x-1）}，则A∩B=（ ）
| A、{x|1≤x＜2} |
| B、{x|x＞2} |
| C、{x|x＞1} |
| D、{x|1＜x＜2} |
已知f（x）=x2+1，对任意x∈（0，+∞），f（
）-2m2f（x）≤f（x-2）-2f（m）恒成立，则实数m的取值范围是（ ）
| x |
| m |
A、（-∞，-
| ||||||||
B、（-∞，-
| ||||||||
C、（-∞，-1]∪[
| ||||||||
| D、（-∞，-1]∪[1，+∞） |
已知全集U={1，2，3，4，5，6，7，8，9，10}，集合A={y∈Z|y=log2x，x∈（1，32）}，B={1，2，3}，则A∩∁UB=（ ）
| A、{1，2，3} |
| B、{1，2，3，4} |
| C、{4} |
| D、{4，5} |
过点M（2，1）且在坐标轴上的截距相等的直线共有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
已知两点M（-1，0），N（1，0），若直线y=k（x-2）上至少存在三个点P，使得△MNP是直角三角形，则实数k的取值范围是（ ）
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
| D、[-5，5] |