题目内容
从数字0,1,2,3,…,9中,按由小到大的顺序取出a1,a2,a3,且a2-a1≥2,a3-a2≥2,则不同的取法有( )
| A、20种 | B、35种 |
| C、56种 | D、60种 |
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:令a2′=a2-1,a3′=a3-2≤7,则a2′-a1≥1,a3′-a2′≥1,问题等价于从数字0,1,2,3,…,7中,按由小到大的顺序取出a1,a2′,a3′的取法数,可得结论.
解答:
解:令a2′=a2-1,a3′=a3-2≤7,
则a2′-a1≥1,a3′-a2′≥1,
问题等价于从数字0,1,2,3,…,7中,按由小到大的顺序取出a1,a2′,a3′的取法数,
故
=56种.
故选:C.
则a2′-a1≥1,a3′-a2′≥1,
问题等价于从数字0,1,2,3,…,7中,按由小到大的顺序取出a1,a2′,a3′的取法数,
故
| C | 3 8 |
故选:C.
点评:本题考查排列、组合及简单计数问题,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)=x2+1,对任意x∈(0,+∞),f(
)-2m2f(x)≤f(x-2)-2f(m)恒成立,则实数m的取值范围是( )
| x |
| m |
A、(-∞,-
| ||||||||
B、(-∞,-
| ||||||||
C、(-∞,-1]∪[
| ||||||||
| D、(-∞,-1]∪[1,+∞) |
已知全集U=R,集合A={x|
<0|,B={x|lgx≥0},则集合{x|x≤1}等于( )
| x |
| 1-x |
| A、A∩B |
| B、A∪B |
| C、∁U(A∩B) |
| D、∁U(A∩B) |
过点M(2,1)且在坐标轴上的截距相等的直线共有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
已知△ABC中,|
|=2,A=
,则|
+
|有( )
| BC |
| π |
| 3 |
| AB |
| AC |
A、最大值
| ||
B、最大值2
| ||
C、最小值
| ||
D、最小值2
|
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的部分图象如图所示,则满足a,b关系是( )
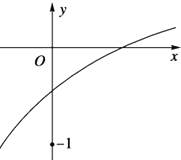

A、0<
| ||||
B、0<b<
| ||||
C、0<
| ||||
D、0<
|