题目内容
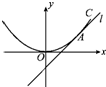 如图,直线l:y=x+b与抛物线x2=4y相切于点A.
如图,直线l:y=x+b与抛物线x2=4y相切于点A.(1)求实数b的值;
(2)若过抛物线的焦点且平行于直线l的直线l1交抛物线于B,C两点,求△ABC的面积.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由直线l:y=x+b与抛物线x2=4y,根据直线l与抛物线相切,可得△=16+16b=0,即可求实数b的值;
(2)由题意可知直线l1的方程为y=x+1,代入抛物线方程,利用弦长公式求出|BC|,求出点A到直线l1的距离,可求△ABC的面积.
(2)由题意可知直线l1的方程为y=x+1,代入抛物线方程,利用弦长公式求出|BC|,求出点A到直线l1的距离,可求△ABC的面积.
解答:
解:(1)由直线l:y=x+b与抛物线x2=4y,消去y,
可$\end{array}\right.$得x2=4(x+b),即x2-4x-4b=0…(2分)
∵直线l与抛物线相切,
∴△=16+16b=0,即b=-1…(5分)
(2)∵抛物线的焦点为(0,1),
∴由题意可知直线l1的方程为y=x+1 …(7分)
由
得x2-4x-4=0…(8分)
设B(x1,y1),C(x2,y2),则x1+x2=4,x1x2=-4,
∴|BC|=
•|x1-x2|=
•
=8…(10分)
由(1)得点的坐标为A(2,1)…(11分)
∴点A到直线l1的距离d=
=
…(12分)
∴S△ABC=
|BC|d=4
…(13分)
可$\end{array}\right.$得x2=4(x+b),即x2-4x-4b=0…(2分)
∵直线l与抛物线相切,
∴△=16+16b=0,即b=-1…(5分)
(2)∵抛物线的焦点为(0,1),
∴由题意可知直线l1的方程为y=x+1 …(7分)
由
|
设B(x1,y1),C(x2,y2),则x1+x2=4,x1x2=-4,
∴|BC|=
| 2 |
| 2 |
| 16+16 |
由(1)得点的坐标为A(2,1)…(11分)
∴点A到直线l1的距离d=
| |2-1+1| | ||
|
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
点评:本题考查直线与抛物线的位置关系,考查弦长公式,考查三角形面积的计算,正确运用韦达定理是关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 已知圆O:x2+y2=m(m>0)与抛物线y2=ax(a>0)相交于A(1,1),B(1,-1)两点.
已知圆O:x2+y2=m(m>0)与抛物线y2=ax(a>0)相交于A(1,1),B(1,-1)两点.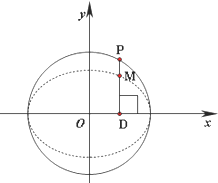 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且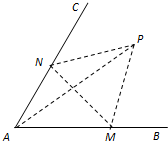 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).