题目内容
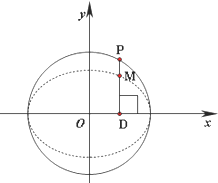 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且| DM |
| ||
| 2 |
| DP |
(Ⅰ)当点P在圆上运动时,求点M的轨迹方程;
(Ⅱ)记(Ⅰ)所得的曲线为C,已知过点N(2,0)的直线l与曲线C相交于两点A、B两点,设Q为曲线C上一点,且满足
| OA |
| OB |
| OQ |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用
=
,确定M,P坐标之间的关系,根据点P在圆上运动,即可求点M的轨迹方程;
(Ⅱ)设出直线方程,和椭圆联立后化为关于x的一元二次方程,由判别式大于0求出k的范围,利用根与系数关系得到A,B两点的横坐标的和与积,代入
+
=t
后得到P点的坐标,把P点坐标代入椭圆方程后得到t与k的关系,由k的范围确定t的范围.
| DM |
| ||
| 2 |
| DP |
(Ⅱ)设出直线方程,和椭圆联立后化为关于x的一元二次方程,由判别式大于0求出k的范围,利用根与系数关系得到A,B两点的横坐标的和与积,代入
| OA |
| OB |
| OQ |
解答:
解:(Ⅰ)设点M的坐标为(x,y),点P的坐标为(x0,y0),则
由
=
,即(0,y)=
(x0-x,y0),得:x0=x,y0=
y,
因为点P在圆x2+y2=2上运动,所以
+
=2.①
把x0=x,y0=
y代入方程①,得x2+2y2=2,即
+y2=1这就是点M的轨迹方程.…5分
(Ⅱ)曲线C的方程为
+y2=1.
由题意知直线l的斜率存在.
设直线l的方程:y=k(x-2),A(x1,y1),B(x2,y2),Q(x,y),…6分
由
得(1+2k2)x2-8k2x+8k2-2=0.…8分
△=64k4-4(2k2+1)(8k2-2)>0,∴k2<
.…9分
∵
+
=t
,
∴(x1+x2,y1+y2)=t(x,y).
∴x=
=
,y=
=
∵点P在椭圆上,∴[
]2+2•[
]2=2.
∴16k2=t2(1+2k2)…11分
∴t2=
=
<
=4,则-2<t<2,…13分
∴t的最大整数值为1.…14分.
由
| DM |
| ||
| 2 |
| DP |
| ||
| 2 |
| 2 |
因为点P在圆x2+y2=2上运动,所以
| x | 2 0 |
| y | 2 0 |
把x0=x,y0=
| 2 |
| x2 |
| 2 |
(Ⅱ)曲线C的方程为
| x2 |
| 2 |
由题意知直线l的斜率存在.
设直线l的方程:y=k(x-2),A(x1,y1),B(x2,y2),Q(x,y),…6分
由
|
△=64k4-4(2k2+1)(8k2-2)>0,∴k2<
| 1 |
| 2 |
∵
| OA |
| OB |
| OP |
∴(x1+x2,y1+y2)=t(x,y).
∴x=
| x1+x2 |
| t |
| 8k2 |
| t(1+2k2) |
| y1+y2 |
| t |
| -4k |
| t(1+2k2) |
∵点P在椭圆上,∴[
| 8k2 |
| t(1+2k2) |
| -4k |
| t(1+2k2) |
∴16k2=t2(1+2k2)…11分
∴t2=
| 16k2 |
| 1+2k2 |
| 16 | ||
|
| 16 |
| 2+2 |
∴t的最大整数值为1.…14分.
点评:本题考查了椭圆的简单几何性质,考查了直线与圆锥曲线的关系,考查了平面向量的坐标运算,训练了利用代入法求解变量的取值范围.属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
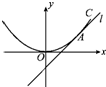 如图,直线l:y=x+b与抛物线x2=4y相切于点A.
如图,直线l:y=x+b与抛物线x2=4y相切于点A.