Question

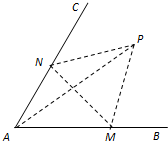如图，经过村庄A有两条夹角为60°的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M、N （异于村庄A），要求PM=PN=MN=2（单位：千米）．如何设计，使得工厂产生的噪声对居民的影响最小（即工厂与村庄的距离最远）．

Answer 1

考点：解三角形的实际应用

专题：综合题,解三角形

分析：设∠AMN=θ，在△AMN中，求出AM，在△APM中，利用余弦定理，建立函数，利用辅助角公式化简，即可得出结论．

解答： 解：设∠AMN=θ，在△AMN中，

MN

sin60°

=

AM

sin(120°-θ)

．
因为MN=2，所以AM=

4 3

3

sin（120°-θ）．               …2分
在△APM中，cos∠AMP=cos（60°+θ）．                 …6分
AP²=AM²+MP²-2AM•MP•cos∠AMP
=

16

3

sin²（120°-θ）+4-2×2×

4 3

3

 sin（120°-θ） cos（60°+θ）         …8分
=

16

3

sin²（θ+60°）-

16 3

3

 sin（θ+60°） cos（θ+60°）+4
=

8

3

[1-cos （2θ+120°）]-

8 3

3

 sin（2θ+120°）+4
=-

8

3

[

3

sin（2θ+120°）+cos （2θ+120°）]+

20

3

=

20

3

-

16

3

sin（2θ+150°），θ∈（0，120°）．                 …12分
当且仅当2θ+150°=270°，即θ=60°时，AP²取得最大值12，即AP取得最大值2

3

．
答：设计∠AMN为60°时，工厂产生的噪声对居民的影响最小．…14分

点评：本题考查正弦定理、余弦定理的运用，考查三角函数的化简，正确构建函数是关键．