题目内容
已知关于x的函数y=3x2+2(a-1)x+a2,-1≤x≤1,
(1)求此函数的最小值;
(2)若函数值的最小值为13,求a的值.
(1)求此函数的最小值;
(2)若函数值的最小值为13,求a的值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据二次函数的图象和性质,分析函数图象的开口方向和对称轴,进而
<-1,即a>4时,-1≤
≤1,即-2≤a≤4时和
>1,即a<-2时,三种情况,可以分析出函数的最小值;
(2)根据已知中函数值的最小值为13,结合(1)中的三种情况分类讨论,最后综合讨论结果,可得答案.
| 1-a |
| 3 |
| 1-a |
| 3 |
| 1-a |
| 3 |
(2)根据已知中函数值的最小值为13,结合(1)中的三种情况分类讨论,最后综合讨论结果,可得答案.
解答:
解:(1)∵函数y=3x2+2(a-1)x+a2的图象是开口朝上,且以直线x=
为对称轴抛物线,
若
<-1,即a>4时,当x=-1时,函数取最小值a2-2a+5,
若-1≤
≤1,即-2≤a≤4时,当x=
时,函数取最小值
a2+
a-
,
若
>1,即a<-2时,当x=1时,函数取最小值a2+2a+1;
(2)当
<-1,即a>4时,
若函数取最小值a2-2a+5=13,
解得a=-2,或a=4,均不满足条件;
当-1≤
≤1,即-2≤a≤4时,
若函数取最小值
a2+
a-
=13,
解得a=4,或a=-5(舍去);
当
>1,即a<-2时,
若函数取最小值a2+2a+1=13,
解得a=-1-
,或a=-1+
(舍去),
综上所述满足条件的a值为-1-
或4.
| 1-a |
| 3 |
若
| 1-a |
| 3 |
若-1≤
| 1-a |
| 3 |
| 1-a |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
若
| 1-a |
| 3 |
(2)当
| 1-a |
| 3 |
若函数取最小值a2-2a+5=13,
解得a=-2,或a=4,均不满足条件;
当-1≤
| 1-a |
| 3 |
若函数取最小值
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
解得a=4,或a=-5(舍去);
当
| 1-a |
| 3 |
若函数取最小值a2+2a+1=13,
解得a=-1-
| 13 |
| 13 |
综上所述满足条件的a值为-1-
| 13 |
点评:本题考查的知识点是二次函数的图象和性质,二次函数在定区间上的最值问题,难度中档.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知l,m是两条不同的直线,α是一个平面,且l∥α,则下列命题正确的是( )
| A、若l∥m,则m∥α |
| B、若m∥α,则l∥m |
| C、若l⊥m,则m⊥α |
| D、若m⊥α,则l⊥m |
已知f(x)为R上的偶函数,对任意x∈R都有f(x+6)=f(x)+f(3),x1,x2∈[0,3],x1≠x2时,有
>0成立,下列结论中错误的是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)=0 |
| B、直线x=-6是函数y=f(x)的图象的一条对称轴 |
| C、函数y=f(x)在[-9,9]上有四个零点 |
| D、函数y=f(x)在[-9,-6]上为增函数 |
 已知椭圆
已知椭圆 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈(
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈(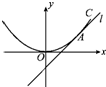 如图,直线l:y=x+b与抛物线x2=4y相切于点A.
如图,直线l:y=x+b与抛物线x2=4y相切于点A.