题目内容
在正数数列{an}中,Sn为an的前n项和,若点(an,Sn)在函数y=
的图象上,其中c为正常数,且c≠1.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足bn=
,当c=2的时候,是否存在正整数m、n(1<m<n),使得b1,bm,bn成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由;
(3)设数列{cn}满足cn=
,k∈N*,当c=
时候,在数列{cn}中,是否存在连续的三项cr,cr+1,cr+2,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数r的值;若不存在,说明理由.
| c2-x |
| c-1 |
(1)求数列{an}的通项公式;
(2)设数列{bn}满足bn=
| n2 nan+2 |
| 2n+1 |
(3)设数列{cn}满足cn=
|
| ||
| 3 |
考点:数列与函数的综合
专题:综合题,等差数列与等比数列
分析:(1)利用点(an,Sn)在函数y=
的图象上,可得Sn=
,再写一式,两式相减,可得数列{an}为等比数列,求出a1=c,即可求数列{an}的通项公式;
(2)bn=
=
,若b1,bm,bn成等比数列,则(
)2=
•
,化简,即可求出所有的m、n的值;
(3)分类讨论,若cr=c2k,不成立;若cr=c2k-1,可得k=3k-1,令Tk=
,则Tk+1-Tk=
<0,即可得出结论.
| c2-x |
| c-1 |
| c2-an |
| c-1 |
(2)bn=
| n2 nan+2 |
| 2n+1 |
| n |
| 2n+1 |
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
(3)分类讨论,若cr=c2k,不成立;若cr=c2k-1,可得k=3k-1,令Tk=
| k |
| 3k-1 |
| 1-2k |
| 3k |
解答:
解:(1)∵点(an,Sn)在函数y=
的图象上,
∴Sn=
,
n≥2时,Sn-Sn-1=an=
,
∴(c-1)an=an-1-an,
∴
=
∴数列{an}为等比数列 2分
将(a1,S1)代入y=
得,a1=c 3分
故an=(
)n-2 4分
(2)bn=
=
.
若b1,bm,bn成等比数列,则(
)2=
•
可得
=
∴-2m2+4m+1>0,解得:1-
<m<1+
又m为正整数且m>1,∴m=2,此时n=12
∴当m=2,n=12,使得b1,bm,bn成等比数列 10分
(3)若cr=c2k,则由cr+cr+2=2cr+1,得2•3k-1+2•3k=2(2k+1),
化简得4•3k-1=2k+1,此式左边为偶数,右边为奇数,不可能成立. 12分
若cr=c2k-1,则由cr+cr+2=2cr+1,得(2k-1)+(2k+1)=2•2•3k-1
化简得k=3k-1. 14分
令Tk=
,则Tk+1-Tk=
<0
因此,1=T1>T2>T3>…,
故只有T1=1,此时r=2×1-1=1,
综上,在数列{cn}中,仅存在连续的三项cr,cr+1,cr+2,按原来的顺序成等差数列,此时正整数r=1.16分
| c2-x |
| c-1 |
∴Sn=
| c2-an |
| c-1 |
n≥2时,Sn-Sn-1=an=
| an-1-an |
| c-1 |
∴(c-1)an=an-1-an,
∴
| an |
| an-1 |
| 1 |
| c |
∴数列{an}为等比数列 2分
将(a1,S1)代入y=
| c2-x |
| c-1 |
故an=(
| 1 |
| c |
(2)bn=
| n2 nan+2 |
| 2n+1 |
| n |
| 2n+1 |
若b1,bm,bn成等比数列,则(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
可得
| 3 |
| n |
| -2m2+4m+1 |
| m2 |
∴-2m2+4m+1>0,解得:1-
| ||
| 2 |
| ||
| 2 |
又m为正整数且m>1,∴m=2,此时n=12
∴当m=2,n=12,使得b1,bm,bn成等比数列 10分
(3)若cr=c2k,则由cr+cr+2=2cr+1,得2•3k-1+2•3k=2(2k+1),
化简得4•3k-1=2k+1,此式左边为偶数,右边为奇数,不可能成立. 12分
若cr=c2k-1,则由cr+cr+2=2cr+1,得(2k-1)+(2k+1)=2•2•3k-1
化简得k=3k-1. 14分
令Tk=
| k |
| 3k-1 |
| 1-2k |
| 3k |
因此,1=T1>T2>T3>…,
故只有T1=1,此时r=2×1-1=1,
综上,在数列{cn}中,仅存在连续的三项cr,cr+1,cr+2,按原来的顺序成等差数列,此时正整数r=1.16分
点评:本题考查数列与函数的综合,考查等比数列的判断,考查数列的通项,考查分类讨论的数学思想,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
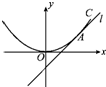 如图,直线l:y=x+b与抛物线x2=4y相切于点A.
如图,直线l:y=x+b与抛物线x2=4y相切于点A.