题目内容
 已知圆O:x2+y2=m(m>0)与抛物线y2=ax(a>0)相交于A(1,1),B(1,-1)两点.
已知圆O:x2+y2=m(m>0)与抛物线y2=ax(a>0)相交于A(1,1),B(1,-1)两点.(1)求圆O的半径,抛物线的焦点坐标及准线方程;
(2)设P是抛物线上不同于A,B的点,且在圆外部,PA的延长线交圆于点C,直线PB与x轴交于点D,点E在直线PB上,且四边形ODEC为等腰梯形,求点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据A(1,1)在圆O:x2+y2=m上,可求圆O的半径;A(1,1)代入抛物线y2=ax,可得a=1,从而可求抛物线的焦点坐标及准线方程;
(2)设P(m,n),由四边形ODEC为等腰梯形,可得kOC=kPB=
,从而可得OC的方程为y=-
x,代入圆的方程,求出C的坐标,利用P,A,C三点共线,即可得出结论.
(2)设P(m,n),由四边形ODEC为等腰梯形,可得kOC=kPB=
| n+1 |
| m-1 |
| n+1 |
| m-1 |
解答:
解:(1)∵A(1,1)在圆O:x2+y2=m上,
∴圆O的半径为
,
A(1,1)代入抛物线y2=ax,可得a=1,
∴抛物线的方程为y2=x,
∴抛物线的焦点坐标(
,0),准线方程:x=-
;
(2)设P(m,n),则
∵四边形ODEC为等腰梯形,
∴kOC=kPB=
,
∴OC的方程为y=-
x,
代入x2+y2=2,可得x=-
,y=
•
,
∵P,A,C三点共线,
∴
=
,
∵n2=m,
∴可得P的坐标为:(8+2
,1+
)或(8-2
,1-
).
∴圆O的半径为
| 2 |
A(1,1)代入抛物线y2=ax,可得a=1,
∴抛物线的方程为y2=x,
∴抛物线的焦点坐标(
| 1 |
| 4 |
| 1 |
| 4 |
(2)设P(m,n),则
∵四边形ODEC为等腰梯形,
∴kOC=kPB=
| n+1 |
| m-1 |
∴OC的方程为y=-
| n+1 |
| m-1 |
代入x2+y2=2,可得x=-
|
| n+1 |
| m-1 |
|
∵P,A,C三点共线,
∴
| n-1 |
| m-1 |
| ||||||||
-
|
∵n2=m,
∴可得P的坐标为:(8+2
| 7 |
| 7 |
| 7 |
| 7 |
点评:本题考查圆的方程、抛物线的方程与性质,考查直线与圆的位置关系,考查学生的计算能力,属于难题.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知f(x)为R上的偶函数,对任意x∈R都有f(x+6)=f(x)+f(3),x1,x2∈[0,3],x1≠x2时,有
>0成立,下列结论中错误的是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)=0 |
| B、直线x=-6是函数y=f(x)的图象的一条对称轴 |
| C、函数y=f(x)在[-9,9]上有四个零点 |
| D、函数y=f(x)在[-9,-6]上为增函数 |
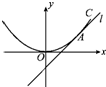 如图,直线l:y=x+b与抛物线x2=4y相切于点A.
如图,直线l:y=x+b与抛物线x2=4y相切于点A.