题目内容
已知f(x)=
,
(1)求f(0)和f[f(-1)]的值;
(2)画出函数草图;
(3)求使f(x)<2的x值的集合.
|
(1)求f(0)和f[f(-1)]的值;
(2)画出函数草图;
(3)求使f(x)<2的x值的集合.
考点:分段函数的应用
专题:计算题,作图题,函数的性质及应用,不等式的解法及应用
分析:(1)由分段函数的表达式即可得到f(0)和f[f(-1)]的值;
(2)画出函数的图象,注意各段的范围及端点的情况;
(3)当x<0时,有2x+3<2;当x≥0时,有2x2+1<2.分别解出它们,最后求并集即可.
(2)画出函数的图象,注意各段的范围及端点的情况;
(3)当x<0时,有2x+3<2;当x≥0时,有2x2+1<2.分别解出它们,最后求并集即可.
解答:
 解:(1)由于f(x)=
解:(1)由于f(x)=
,
则f(0)=1,
f[f(-1)]=f(1)=3;
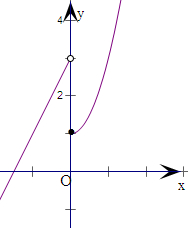
(2)图象如右:
(3)当x<0时,令2x+3<2的x<-
,适合x<0;
当x≥0时,令2x2+1<2得-
x<
,结合x≥0得0≤x<
;
综上述可得x的范围是(-∞,0)∪[0,
).
 解:(1)由于f(x)=
解:(1)由于f(x)=
|
则f(0)=1,
f[f(-1)]=f(1)=3;
(2)图象如右:
(3)当x<0时,令2x+3<2的x<-
| 1 |
| 2 |
当x≥0时,令2x2+1<2得-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
综上述可得x的范围是(-∞,0)∪[0,
| ||
| 2 |
点评:本题考查分段函数及应用,考查分段函数值和图象,以及解不等式,注意各段的自变量的范围是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=
如图所示,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=