题目内容
在△ABC中，若cos（
+A）sin（
+B）tan（C-π）＜0，求证：△ABC是钝角三角形．
| π |
| 2 |
| 3π |
| 2 |
考点：三角函数值的符号,运用诱导公式化简求值
专题：三角函数的求值
分析：根据异名角的转化原式转化为sinAcosBtanC＜0，再根据三角函数值的正负，得出三角形的形状．
解答：
证明：∵cos（
+A）sin（
+B）tan（C-π）＜0，
∴sinAcosBtanC＜0，
∵sinA＞0，
∴cosB和tanC有一个是负数，
∴B，C有一个是钝角，A是锐角，
∴△ABC是钝角三角形．
| π |
| 2 |
| 3π |
| 2 |
∴sinAcosBtanC＜0，
∵sinA＞0，
∴cosB和tanC有一个是负数，
∴B，C有一个是钝角，A是锐角，
∴△ABC是钝角三角形．
点评：本题考查三角形的形状判断，着重考查异名角的转化，属于基础题
练习册系列答案
相关题目
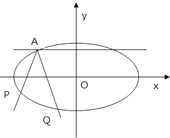如图，焦点在x轴的椭圆，离心率A，且过点A（-2，1），由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点（Q点与P点不重合）．