题目内容
已知椭圆C:
+
=1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线x+y+1=0与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(1)求椭圆的方程.
(2)设P为椭圆上一点,若过点M(2,0)的直线l与椭圆E相交于不同的两点S和T,且满足
+
=t
(O为坐标原点),求实数t的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程.
(2)设P为椭圆上一点,若过点M(2,0)的直线l与椭圆E相交于不同的两点S和T,且满足
| OS |
| OT |
| OP |
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)写出满足条件的圆的方程,再由直线与圆相切得到d=a,再由等腰直角三角形得到b=c,解方程即可得到a,b的值;
(2)设P(x0,y0),设出直线l:y=k(x-2),联立椭圆方程消去y,得到x的方程,运用韦达定理和判别式大于0,再由向量加法运算得到x0,y0的关系,代入椭圆方程,结合判别式大于0,即可得到t的范围.
(2)设P(x0,y0),设出直线l:y=k(x-2),联立椭圆方程消去y,得到x的方程,运用韦达定理和判别式大于0,再由向量加法运算得到x0,y0的关系,代入椭圆方程,结合判别式大于0,即可得到t的范围.
解答:
解:(1)由题意得,以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径
的圆的方程为(x-c)2+y2=a2,
∴圆心到直线x+y+1=0的距离d=
=a*,
∵椭圆C:
+
=1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,
则b=c,a=
b=
c,代入*式得b=c=1即a=
b=
,
故所求椭圆方程为
+y2=1;
(2)由题意知直线l的斜率存在,设直线l方程为y=k(x-2),设P(x0,y0),
将直线方程代入椭圆方程得:(1+2k2)x2-8k2x+8k2-2=0,
∴△=64k4-4(1+2k2)(8k2-2)=-16k2+8>0
∴k2<
,
设S(x1,y1),T(x2,y2)则x1+x2=
,x1x2=
,
当k=0时,直线l的方程为y=0,此时t=0,
+
=t
成立,故t=0符合题意.
当t≠0时
得tx0=x1+x2=
,ty0=y1+y2=k(x1+x2)-4k=
,
∴x0=
•
,y0=
•
,
将上式代入椭圆方程得:
+
=1,
整理得:t2=
由k2<
知0<t2<4,
所以t∈(-2,2).
的圆的方程为(x-c)2+y2=a2,
∴圆心到直线x+y+1=0的距离d=
| |c+1| | ||
|
∵椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
则b=c,a=
| 2 |
| 2 |
| 2 |
| 2 |
故所求椭圆方程为
| x2 |
| 2 |
(2)由题意知直线l的斜率存在,设直线l方程为y=k(x-2),设P(x0,y0),
将直线方程代入椭圆方程得:(1+2k2)x2-8k2x+8k2-2=0,
∴△=64k4-4(1+2k2)(8k2-2)=-16k2+8>0
∴k2<
| 1 |
| 2 |
设S(x1,y1),T(x2,y2)则x1+x2=
| 8k2 |
| 1+2k2 |
| 8k2-2 |
| 1+2k2 |
当k=0时,直线l的方程为y=0,此时t=0,
| OS |
| OT |
| OP |
当t≠0时
得tx0=x1+x2=
| 8k2 |
| 1+2k2 |
| -4k |
| 1+2k2 |
∴x0=
| 1 |
| t |
| 8k2 |
| 1+2k2 |
| 1 |
| t |
| -4k |
| 1+2k2 |
将上式代入椭圆方程得:
| 32k4 |
| t2(1+2k2)2 |
| 16k2 |
| t2(1+2k2)2 |
整理得:t2=
| 16k2 |
| 1+2k2 |
由k2<
| 1 |
| 2 |
所以t∈(-2,2).
点评:本题考查椭圆的方程和性质,以及直线与圆相切的条件,考查联立直线方程和椭圆方程消去一个未知数,运用韦达定理,注意判别式大于0的条件,考查运算能力,属于中档题.

练习册系列答案
相关题目
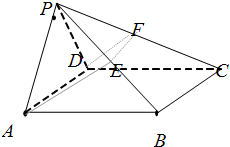 四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形.
四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形.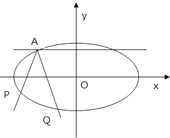 如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).
如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).