题目内容
(1)函数y=
的值域是
(2)函数y=x2+x(-1≤x≤3)的值域是 .
| -2 |
| x |
(2)函数y=x2+x(-1≤x≤3)的值域是
考点:函数的值域
专题:函数的性质及应用
分析:画出函数图象,利用图象求函数的值域.
解答:
(1)函数y=
,图象如下图:

根据图象可以看出值域为:(-∞,0)∪(0,+∞).
(2)函数y=x2+x(-1≤x≤3),图象如下图,

当x=-
时,y=-
,
函数y=x2+x(-1≤x≤3)的值域是[-
,12]
| -2 |
| x |

根据图象可以看出值域为:(-∞,0)∪(0,+∞).
(2)函数y=x2+x(-1≤x≤3),图象如下图,

当x=-
| 1 |
| 2 |
| 1 |
| 4 |
函数y=x2+x(-1≤x≤3)的值域是[-
| 1 |
| 4 |
点评:本题考查了数形结合的思想,运用函数的图象解决函数值域问题.

练习册系列答案
相关题目
设函数y=f(x)在R上有意义,对给定正数M,定义函数fM(x)=
,则称函数fM(x)为f(x)的“孪生函数”,若给定函数f(x)=2-x2,M=1,则y=fM(x)的值域为( )
|
| A、[1,2] |
| B、[-1,2] |
| C、(-∞,2] |
| D、(-∞,1] |
已知a,b是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A、若a∥b,b?α,则a∥α |
| B、若a∥α,b?α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a⊥b,b⊥α,则a∥α |
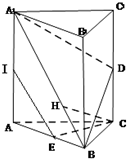 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.