题目内容
设函数f(x)=-x(x-a)2(x∈R),其中a∈R.
(Ⅰ)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)当a>0时,求函数f(x)的极大值和极小值;
(Ⅲ)当a>3时,在区间[-1,0]上是否有实数k使不等式f(k-cosx)≥f(k2-cos2x),对任意的x∈R恒成立,若存在,求出k的值,若不存在,说明理由.
(Ⅰ)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)当a>0时,求函数f(x)的极大值和极小值;
(Ⅲ)当a>3时,在区间[-1,0]上是否有实数k使不等式f(k-cosx)≥f(k2-cos2x),对任意的x∈R恒成立,若存在,求出k的值,若不存在,说明理由.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(I)利用导数的几何意义可得切线的斜率f′(2)=-5.再利用点斜式即可得出;
(II)令f′(x)=0,解得x=
或x=a.列出表格研究函数的大小,即可得出极值;
(III)假设在区间[-1,0]上存在实数k满足题意.由a>3,得
>1,由(Ⅱ)知,f(x)在(-∞,1]上是减函数,当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.要使f(k-cosx)≥f(k2-cos2x),x∈R只要k-cosx≤k2-cos2x(x∈R)即cos2x-cosx≤k2-k(x∈R),再利用二次函数与余弦函数的单调性即可得出.
(II)令f′(x)=0,解得x=
| a |
| 3 |
(III)假设在区间[-1,0]上存在实数k满足题意.由a>3,得
| a |
| 3 |
解答:
解:(I)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,得f(2)=-2,
且f′(x)=-3x2+4x-1,∴f′(2)=-5.
∴曲线y=-x(x-1)2在点(2,-2)处的切线方程是y+2=-5(x-2),
整理得5x+y-8=0.
(Ⅱ)解:f(x)=-x(x-a)2=-x3+2ax2-a2x,
∴f′(x)=-3x2+4ax-a2=-(3x-a)(x-a).
令f′(x)=0,解得x=
或x=a.
由于a>0,当x变化时,且f′(x)的正负如下表:
因此,函数f(x)在x=
处取得极小值f(
),且f(
)=-
a3;
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
(Ⅲ)假设在区间[-1,0]上存在实数k满足题意.
由a>3,得
>1,由(Ⅱ)知,f(x)在(-∞,1]上是减函数,
当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.
要使f(k-cosx)≥f(k2-cos2x),x∈R
只要k-cosx≤k2-cos2x(x∈R)
即cos2x-cosx≤k2-k(x∈R)①
设g(x)=cos2x-cosx=(cosx-
)2-
,则函数g(x)在R上的最大值为2.
要使①式恒成立,必须k2-k≥2,即k≥2或k≤-1.
∴在区间[-1,0]上存在k=-1,使得f(k-cosx)≥f(k2-cos2x)对任意的x∈R恒成立.
且f′(x)=-3x2+4x-1,∴f′(2)=-5.
∴曲线y=-x(x-1)2在点(2,-2)处的切线方程是y+2=-5(x-2),
整理得5x+y-8=0.
(Ⅱ)解:f(x)=-x(x-a)2=-x3+2ax2-a2x,
∴f′(x)=-3x2+4ax-a2=-(3x-a)(x-a).
令f′(x)=0,解得x=
| a |
| 3 |
由于a>0,当x变化时,且f′(x)的正负如下表:
| x | (-∞,
|
| (
| a | (a,+∞) | ||||||
| f'(x) | - | 0 | + | 0 | - |
| a |
| 3 |
| a |
| 3 |
| a |
| 3 |
| 4 |
| 27 |
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
(Ⅲ)假设在区间[-1,0]上存在实数k满足题意.
由a>3,得
| a |
| 3 |
当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.
要使f(k-cosx)≥f(k2-cos2x),x∈R
只要k-cosx≤k2-cos2x(x∈R)
即cos2x-cosx≤k2-k(x∈R)①
设g(x)=cos2x-cosx=(cosx-
| 1 |
| 2 |
| 1 |
| 4 |
要使①式恒成立,必须k2-k≥2,即k≥2或k≤-1.
∴在区间[-1,0]上存在k=-1,使得f(k-cosx)≥f(k2-cos2x)对任意的x∈R恒成立.
点评:本题考查了利用导数研究函数的单调性极值与最值、切线方程,考查了二次函数与余弦函数的单调性,考查了分类讨论、分离参数的方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
函数y=x+
在x=1处的导数是( )
| 1 |
| x |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、0 |
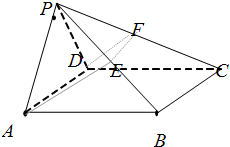 四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形.
四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形.