题目内容
 如图所示,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=
如图所示,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=考点:与圆有关的比例线段
专题:立体几何
分析:由已知条件推导出△ABC∽△CDE,从而BC2=AB•DE=12,由此能求出BC的值.
解答:
解:∵AB是直径,BC=CD,
∴AC⊥BC,∴∠B=∠D,
CE是切线,∠DCE=∠DAC,
∴∠CED=∠ACD=90°,∠ACB=∠CED=90°,
∴△ABC∽△CDE,
=
,又BC=CD,
∴BC2=AB•DE=12,
∴BC=2
.
故答案为:2
.
∴AC⊥BC,∴∠B=∠D,
CE是切线,∠DCE=∠DAC,
∴∠CED=∠ACD=90°,∠ACB=∠CED=90°,
∴△ABC∽△CDE,
| AB |
| CD |
| BC |
| DE |
∴BC2=AB•DE=12,
∴BC=2
| 3 |
故答案为:2
| 3 |
点评:本题考查线段长的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x.若在区间[-2,2]上方程ax+a-f(x)=0恰有三个不相等的实数根,则实数a的取值范围是( )
| A、[0,1) |
| B、[0,2] |
| C、[1,+∞) |
| D、[2,+∞) |
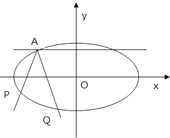 如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).
如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).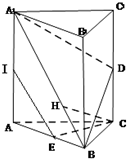 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.