题目内容
已知集合A={x|
<1},B={x|-x2+x-m+m2≥0},若满足A∪B=A,求实数m取值范围.
| 1 |
| x-3 |
考点:并集及其运算
专题:集合
分析:求
<1的解集即求出A,由-x2+x-m+m2≥0得(x-m)[x-(1-m)]≤0,求出两个集合B,由A∪B=A可得B⊆A,再根据子集的定义分别列出不等式,求出m的范围,最后把各个部分的结果并在一起.
| 1 |
| x-3 |
解答:
解:由
<1得,
<0,则(x-3)(x-4)>0,
解得x>4或x<3,∴A={x|x>4或x<3},
由-x2+x-m+m2≥0得,x2-x+m-m2≤0,则(x-m)[x-(1-m)]≤0,
解得:m≤x≤1-m或1-m≤x≤m,
则B={x|m≤x≤1-m}或B={x|1-m≤x≤m},
∵A∪B=A,∴B⊆A,
当B={x|m≤x≤1-m}时,有m>1-m或
或
,
解得m>
或-2<m≤
,即m>-2;
当B={x|1-m≤x≤m}时,有1-m>m或
或
,
解得m<
或
≤m<3,即m<3,
综上得,m>-2或m<3,即实数m取值范围是R.
| 1 |
| x-3 |
| 4-x |
| x-3 |
解得x>4或x<3,∴A={x|x>4或x<3},
由-x2+x-m+m2≥0得,x2-x+m-m2≤0,则(x-m)[x-(1-m)]≤0,
解得:m≤x≤1-m或1-m≤x≤m,
则B={x|m≤x≤1-m}或B={x|1-m≤x≤m},
∵A∪B=A,∴B⊆A,
当B={x|m≤x≤1-m}时,有m>1-m或
|
|
解得m>
| 1 |
| 2 |
| 1 |
| 2 |
当B={x|1-m≤x≤m}时,有1-m>m或
|
|
解得m<
| 1 |
| 2 |
| 1 |
| 2 |
综上得,m>-2或m<3,即实数m取值范围是R.
点评:本题考查集合的并集的性质与运算,分式不等式的求解,一元二次不等式的求解问题,涉及集合中含参数的问题,以及分类讨论思想,关键是解不等式求出集合A、B,以及正确进行分类.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
方程x2+ky2=1表示焦点在y轴上的椭圆,则k的范围( )
| A、(0,+∞) |
| B、(0,2) |
| C、(0,1) |
| D、(1,+∞) |
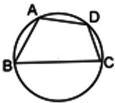 为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.
为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.