题目内容
已知命题P:方程x2+2ax+2-a=0有实数解.命题q:?x∈[1,2],a≥x2,若“p且q”为真命题,求实数a的取值范围.
考点:复合命题的真假,全称命题
专题:简易逻辑
分析:命题p:方程x2+2ax+2-a=0有实数解,可得△≥0,解得a的取值范围.命题q::?x∈[1,2],a≥x2,解得a的取值范围.由于命题p∧q为真命题,可得命题p与q都为真命题,求其交集即可.
解答:
解:命题p:方程x2+2ax+2-a=0有实数解,可得,△=4a2-8+4a≥0,解得a≤-2或a≥1.
命题q::?x∈[1,2],a≥x2,解得a≥4.
∵命题p∧q为真命题,∴命题p与q都为真命题,解得4≤a.
∴实数a的取值范围是[4,+∞).
命题q::?x∈[1,2],a≥x2,解得a≥4.
∵命题p∧q为真命题,∴命题p与q都为真命题,解得4≤a.
∴实数a的取值范围是[4,+∞).
点评:本题考查了一元二次方程的实数根与判别式的关系、一元二次不等式的解法、复合命题真假的判定方法,考查了推理能力和计算能力,属于基础题

练习册系列答案
相关题目
已知圆的圆心是(-3,4),半径长是
,则圆的标准方程为( )
| 5 |
| A、(x+3)2+(y-4)2=5 |
| B、(x-3)2+(y-4)2=5 |
| C、(x+3)2+(y-4)2=25 |
| D、(x+3)2+(y+4)2=25 |
 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=4,DC=6,BC=2.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=4,DC=6,BC=2.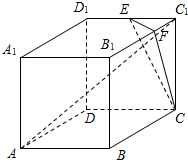 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2