题目内容
已知二次函数f(x)=x2+bx+c
(1)若f(x+1)-f(x)=2x,且f(0)=1.求f(x)的解析式,并求f(x)在区间[0,2]上的最大值与最小值.
(2)若y=f(x)-2x在[5,20]上具有单调性,求实数b的范围.
(1)若f(x+1)-f(x)=2x,且f(0)=1.求f(x)的解析式,并求f(x)在区间[0,2]上的最大值与最小值.
(2)若y=f(x)-2x在[5,20]上具有单调性,求实数b的范围.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:(1)由f(0)=1,求得c的值,f(x)=x2+bx+1;由f(x+1)-f(x)=2x,求得b的值,可得f(x)的解析式.再利用二次函数的性质求得f(x)在区间[0,2]上的最大值与最小值.
(2)根据y=f(x)-2x 的图象的对称轴方程为x=
,分函数在[5,20]上是增函数和函数在[5,20]上是减函数两种情况,分别求得b的范围,再取并集,即得所求.
(2)根据y=f(x)-2x 的图象的对称轴方程为x=
| 2-b |
| 2 |
解答:
解:(1)∵f(0)=c=1,∴c=1,f(x)=x2+bx+1,
∴f(x+1)-f(x)=[(x+1)2+b(x+1)+1]-[x2+bx+1]=2x+b+1=2x,
∴b=-1,f(x)=x2-x+1=(x-
)2+
,
∵x∈[0,2],∴当x=
时,f(x)取得最小值为
,当x=2时,f(x)取得最大值为 3.
(2)∵y=f(x)-2x=x2+(b-2)x+c的图象的对称轴方程为x=
,且函数在[5,20]上具有单调性,
若函数在[5,20]上是增函数,则有
≤5,求得b≥-8.
若函数在[5,20]上是减函数,则有
≥20,求得b≤-38.
综上得:b的取值范围是(-∞,-38]∪[-8,+∞).
∴f(x+1)-f(x)=[(x+1)2+b(x+1)+1]-[x2+bx+1]=2x+b+1=2x,
∴b=-1,f(x)=x2-x+1=(x-
| 1 |
| 2 |
| 3 |
| 4 |
∵x∈[0,2],∴当x=
| 1 |
| 2 |
| 3 |
| 4 |
(2)∵y=f(x)-2x=x2+(b-2)x+c的图象的对称轴方程为x=
| 2-b |
| 2 |
若函数在[5,20]上是增函数,则有
| 2-b |
| 2 |
若函数在[5,20]上是减函数,则有
| 2-b |
| 2 |
综上得:b的取值范围是(-∞,-38]∪[-8,+∞).
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
 如图,在△ABC中,M是AC的中点,点E在AB上,且AE=
如图,在△ABC中,M是AC的中点,点E在AB上,且AE=| 1 |
| 4 |
| A、2:1 | B、3:1 |
| C、3:2 | D、4:1 |
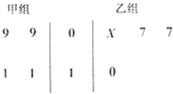 如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.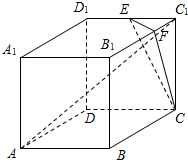 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2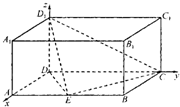 (文科)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.
(文科)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.