题目内容

解方程 lgx+lg（x+3）=1．
考点：对数的运算性质
专题：计算题
分析：由和的对数等于对数的和，然后去掉对数符号后求解一元二次方程得答案．
解答： 解：由 lgx+lg（x+3）=1，
得
x＞0
x+3＞0
x(x+3)=10
，解得x=2．
经检验x=2是原方程的根．
故方程lgx+lg（x+3）=1的根是 2．
点评：本题考查了对数的运算性质，考查了对数方程的解法，是基础题．
练习册系列答案
相关题目
设全集U=R，集合M={x|x＞1}，P={x|x2＞1}，则下列关系中正确的是（　　）
A、M=P
B、P?M
C、∁U（M∩P）=∅
D、M?P
已知圆的圆心是（-3，4），半径长是
5
，则圆的标准方程为（　　）
A、（x+3）2+（y-4）2=5
B、（x-3）2+（y-4）2=5
C、（x+3）2+（y-4）2=25
D、（x+3）2+（y+4）2=25
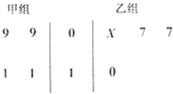如图茎叶图记录了甲、乙两个组四名同学的植树棵树．乙组记录中有一个数计模糊，无法确认，在图中以X表示．
（1）求甲组同学植树的方差；
（2）乙组同学植树的方差会不会小于甲组同学植树的方差？请说明理由．
正数x，y满足
1
x
+
9
y
=1．
（1）求xy的最小值．
（2）求x+y的最小值．
已知向量
b
=（m，sin2x），
c
=（cos2x，n），x∈R，f（x）=
b
•
c
，若函数f（x）的图象经过点（0，1）和（
π
4
，1）．
（1）求m、n的值；
（2）求f（x）的最小正周期，并求f（x）在x∈[0，
π
4
]上的最小值．
已知函数f（x）=2sin（ωx+
π
6
），ω∈R，且ω≠0．
（Ⅰ）若f（x）的图象经过点（
π
6
，2），且0＜ω＜3，求ω的值；
（Ⅱ）在（Ⅰ）的条件下，若函数g（x）=mf（x）+n（m＞0），当x∈[0，
π
2
]时，g（x）的值域为[-5，1]，求m，n的值；
（Ⅲ）若函数h（x）=f（x-
π
6ω
）在[-
π
3
，
π
3
]上是减函数，求ω的取值范围．
已知集合A={x|
1
x-3
＜1}，B={x|-x2+x-m+m2≥0}，若满足A∪B=A，求实数m取值范围．
在数列{an}中，a1=1，an+1=an+c（c为常数，n∈N*），a1，a2，a5构成公比不等于1的等比数列．记bn=
1
anan+1
（n∈N*）．
（Ⅰ）求c的值；
（Ⅱ）设{bn}的前n项和为Rn，是否存在正整数k，使得Rk≥2k成立？若存在，找出一个正整数k；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网