题目内容
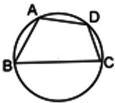 为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.
为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.(Ⅰ)请计算原花圃用地ABCD的面积及圆面的半径R的值;
(Ⅱ)因地理条件的限制,边界AD,CD不能变更,而边界AB,BC可以调整,为提高花圃改造用地的利用率,请在圆弧ABC上设计一点P,使得花圃改造的新用地APCD的面积最大,并求最大值.
考点:函数的最值及其几何意义,函数解析式的求解及常用方法
专题:计算题,应用题,函数的性质及应用
分析:(1)连接AC,应用余弦定理及同角三角函数关系、面积公式求解;(2)当点P在圆弧ABC上的中点时,新用地APCD的面积最大,求三角形的高,然后求面积.
解答:
解:(Ⅰ)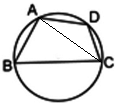 连接AC,则由∠B+∠D=π得,
连接AC,则由∠B+∠D=π得,
cosB+cosD=0,
即
+
=0,
即
+
=0,
解得,AC=2
,cosB=
,
∴sinB=sinD=
,
SABCD=
•AB•BC•SinB+
AD•DC•DC•sinD
=
×4×6×
+
×4×2×
=8
.
R=
•
=
.
(Ⅱ)由图可知,当点P在圆弧ABC上的中点时,新用地APCD的面积最大,
此时,点P到AC的距离为h=
+
=
,
则面积为S=
•AC•h+sACD=
×2
×
+2
=9
.
 连接AC,则由∠B+∠D=π得,
连接AC,则由∠B+∠D=π得,cosB+cosD=0,
即
| AB2+BC2-AC2 |
| 2AB•BC |
| AD2+DC2-AC2 |
| 2AD•DC |
即
| 16+36-AC2 |
| 2×4×6 |
| 16+4-AC2 |
| 2×4×2 |
解得,AC=2
| 7 |
| 1 |
| 2 |
∴sinB=sinD=
| ||
| 2 |
SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
R=
| AC |
| SinB |
| 1 |
| 2 |
2
| ||
| 3 |
(Ⅱ)由图可知,当点P在圆弧ABC上的中点时,新用地APCD的面积最大,
此时,点P到AC的距离为h=
2
| ||
| 3 |
(
|
| 21 |
则面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 21 |
| 3 |
| 3 |
点评:四边形的面积有时化为三角形求解,本题还考查了解三解形的知识.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
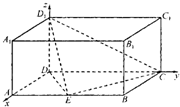 (文科)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.
(文科)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.
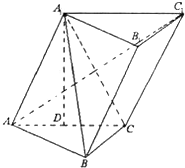 如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D.
如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D.