题目内容
方程x2+ky2=1表示焦点在y轴上的椭圆，则k的范围（ ）
| A、（0，+∞） |
| B、（0，2） |
| C、（0，1） |
| D、（1，+∞） |
考点：椭圆的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：方程化为标准方程，即可得出结论．
解答：
解：方程x2+ky2=1化为方程x2+
=1，
因为方程x2+ky2=1表示焦点在y轴上的椭圆，
所以
＞1，即0＜k＜1．
故选：C．
| y2 | ||
|
因为方程x2+ky2=1表示焦点在y轴上的椭圆，
所以
| 1 |
| k |
故选：C．
点评：熟练掌握椭圆的标准方程及其性质是解题的关键．
练习册系列答案
相关题目
若一个圆的圆心在直线y=2x上，经过点（
，
），且与直线x-y+
=0相切，则这个圆的方程可能是（ ）
| ||
| 2 |
| ||
| 2 |
| 2 |
| A、x2+y2+x-2y=0 |
| B、x2+y2-2x+4y=0 |
| C、x2+y2-1=0 |
| D、x2+y2-2=0 |
设全集U=R，集合M={x|x＞1}，P={x|x2＞1}，则下列关系中正确的是（ ）
| A、M=P |
| B、P?M |
| C、∁U（M∩P）=∅ |
| D、M?P |
如图，在△ABC中，M是AC的中点，点E在AB上，且AE=| 1 |
| 4 |
| A、2：1 | B、3：1 |
| C、3：2 | D、4：1 |
已知函数y=f（x）是定义在R上的偶函数，当x＞0时，f（x）=lnx，那么函数y=f（x）的零点个数为（ ）
| A、一定是2 |
| B、一定是3 |
| C、可能是2也可能是3 |
| D、可能是0 |
下列函数中是偶函数且在（0，1）上单调递减的是（ ）
A、y=-x
| ||
| B、y=x4 | ||
C、y=x
| ||
| D、y=x-2 |
已知圆的圆心是（-3，4），半径长是
，则圆的标准方程为（ ）
| 5 |
| A、（x+3）2+（y-4）2=5 |
| B、（x-3）2+（y-4）2=5 |
| C、（x+3）2+（y-4）2=25 |
| D、（x+3）2+（y+4）2=25 |
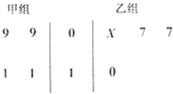如图茎叶图记录了甲、乙两个组四名同学的植树棵树．乙组记录中有一个数计模糊，无法确认，在图中以X表示．