题目内容

已知单位向量
e1
与
e2
的夹角为α，且cosα=
1
3
，向量
a
=3
e1
-2
e2
与
b
=3
e1
-
e2
的夹角为β，求cosβ的值．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量数量积的定义和公式，即可得到结论．
解答： 解：∵单位向量
e1
与
e2
的夹角为α，且cosα=
1
3
，向量
a
=3
e1
-2
e2
与
b
=3
e1
-
e2
的夹角为β，
∴|
a
|2=（3
e1
-2
e2
）2=9
e1
2-12
e1
•
e2
+4
e2
2=9+4-12cosα=9，
∴|
a
|=3，同理|
b
|=2
2
，
a
•
b
=8，
∴cosβ=
a
•
b
|
a
||
b
|
=
8
3×2
2
=
2
2
3
．
点评：本题主要考查向量数量积的应用，根据数量积的公式是解决本题的关键．
练习册系列答案
相关题目
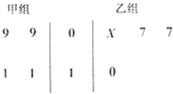如图茎叶图记录了甲、乙两个组四名同学的植树棵树．乙组记录中有一个数计模糊，无法确认，在图中以X表示．
（1）求甲组同学植树的方差；
（2）乙组同学植树的方差会不会小于甲组同学植树的方差？请说明理由．
已知集合A={x|
1
x-3
＜1}，B={x|-x2+x-m+m2≥0}，若满足A∪B=A，求实数m取值范围．
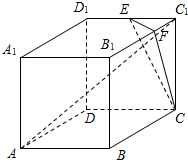如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形，∠DAB=45°，AA1=AB=2，AD=2
2
，点E是 C1D1的中点，点F在B1C1上且B1F=2FC1．
（Ⅰ）证明：AC1⊥平面EFC；
（Ⅱ）求锐二面角A-FC-E平面角的余弦值．
设f（n）=1+
1
2
+
1
3
+…+
1
n
（n∈N），是否存在关于正整数的函数g（n），使等式f（1）+f（2）+…+f（n-1）=g（n）•[f（n）-1]对于n≥2的一切自然数都成立？证明你的结论．
已知公差不为零的等差数列{an}的首项a1=1，且第二项、第五项、第十四项成等比数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足b1=1，an=bn+1-bn，求数列{bn}的通项公式．
在数列{an}中，a1=1，an+1=an+c（c为常数，n∈N*），a1，a2，a5构成公比不等于1的等比数列．记bn=
1
anan+1
（n∈N*）．
（Ⅰ）求c的值；
（Ⅱ）设{bn}的前n项和为Rn，是否存在正整数k，使得Rk≥2k成立？若存在，找出一个正整数k；若不存在，请说明理由．
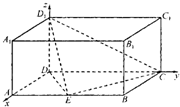（文科）如图，在长方体ABCD-A1B1C1D1中，AD=AA1=2，AB=4，E为AB的中点．分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz．
（Ⅰ）求点E、B1的坐标；
（Ⅱ）求证：D1E⊥CE．
已知tanα=
3
4
，α∈（
π
2
，
3π
2
），求：
（1）
sin(π+α)-sin(
3π
2
+α)
cos(3π-α)+2
；
（2）sin（-
π
4
-α）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网