题目内容
在等比数列{an}中,公比q=2,前99项的和S99=56,则a2+a5+a8+…+a98= .
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由题意和等比数列的前n项和公式得到:a1(299-1)=56,再判断出a2、a5、a8、…、a98成公比为23的等比数列,再由前n项和公式表示出a2+a5+a8+…+a98并化简式子,最后整体代入求值即可.
解答:
解:由题意得,公比q=2,前99项的和S99=56,
所以S99=
=56,即a1(299-1)=56,
因为a2、a5、a8、…、a98成公比为23的等比数列,且一共有33项,
所以a2+a5+a8+…+a98=
=
×a1(299-1)=16,
故答案为:16.
所以S99=
| a1(1-299) |
| 1-2 |
因为a2、a5、a8、…、a98成公比为23的等比数列,且一共有33项,
所以a2+a5+a8+…+a98=
| a2(1-299) |
| 1-23 |
| 2 |
| 7 |
故答案为:16.
点评:本题考查了等比数列的前n项和公式、性质,以及整体思想,属于中档题.

练习册系列答案
相关题目
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为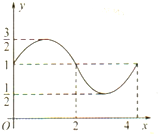 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
到两坐标轴距离相等的点的轨迹方程是( )
| A、y=x |
| B、x2-y2=0 |
| C、y=-x |
| D、y=|x| |
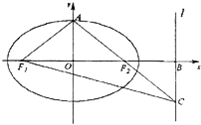 如图,椭圆
如图,椭圆 在如图所示的平面图形中,已知
在如图所示的平面图形中,已知