Question

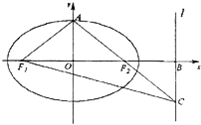如图，椭圆

x2

a2

+

y2

b2

=1的左、右焦点分别为F₁、F₂，A为短轴的一个端点，右准线l与x交于点B，O为坐标原点，若F₂是OB中点．
（1）求椭圆的离心率；
（2）若直线AF₂交l于点C，△AF₁C的面积为2，求椭圆的方程．

Answer 1

考点：椭圆的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：（1）由F₂是OB中点，又由OB=

a2

c

，OF₂=c，可求离心率；
（2）由（1）知，b=c，表示出S=2×

1

2

×2c×c=2，从而求椭圆的方程．

解答： 解：（1）∵F₂是OB中点．
∴

a2

c

=2c，
则e=

c

a

=

2

2

；
（2）∵

c

a

=

2

2

，
∴b=c，
又∵△AF₁C的面积是△AF₁F₂与△CF₁F₂的面积之和，
且A到x轴的距离等于C到x轴的距离，
∴S=2×

1

2

×2c×c=2，
则c=1，
则椭圆的方程为

x2

2

+y2=1．

点评：本题考查了椭圆的方程及椭圆的性质利用，属于中档题．