题目内容
8.一个几何体的三视图如右图所示,其中俯视图是一个正三角形及其内切圆,则该几何体的体积为( )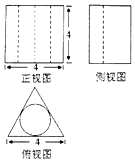
| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |
分析 由三视图得出几何体是一个三棱柱,中间挖去一个内切圆柱,结合图中数据求出体积.
解答 解:由几何体的三视图可得:
该几何体是一个三棱柱,中间挖去一个内切圆柱;
且正三棱柱的底面边长为4,高也为4;
所以组合体的体积为
V=V三棱柱-V圆柱=$\frac{\sqrt{3}}{4}$×42×4-π•${(\frac{1}{3}×\frac{\sqrt{3}}{2}×4)}^{2}$×4=16$\sqrt{3}$-$\frac{16π}{3}$.
故选:A.
点评 本题考查了由三视图求几何体的体积问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设函数f(x)=sin(ωx+φ)(φ>0)的图象关于直线x=-1和x=2对称,则f(0)的取值集合是( )
| A. | {-1,1,-$\frac{1}{2}$} | B. | {1,-$\frac{1}{2}$,$\frac{1}{2}$} | C. | {-1,1,-$\frac{1}{2}$,$\frac{1}{2}$} | D. | {-1,1,-2,2} |
16.已知$\frac{\overline z}{1+2i}=2+i$,则复数z+5的实部与虚部的和为( )
| A. | 10 | B. | -10 | C. | 0 | D. | -5 |
20.某十字路口的信号灯为红灯和绿灯交替出现,红灯持续的时间为60秒,小明放学回家途经该路口遇到红灯,则小明至少要等15秒才能出现绿灯的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
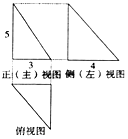
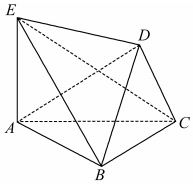 如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.
如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.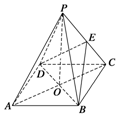 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.