题目内容
18.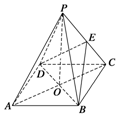 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:PA∥面BDE;
(2)求证:平面PAC⊥平面BDE.
分析 (1)连接OE,由中位线定理可知PA∥OE,故而PA∥面BDE;
(2)由BD⊥OP,BD⊥AC得出BD⊥平面PAC,从而得出平面PAC⊥平面BDE.
解答 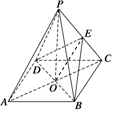 证明:(1)连接OE,
证明:(1)连接OE,
∵ABCD是正方形,O是正方形的中心,
∴O是AC的中点,又E是PC的中点,
∴OE∥PA,
又PA?平面BDE,OE?平面BDE,
∴PA∥面BDE.
(2)∵PO⊥底面ABCD,BD?平面ABCD,
∴PO⊥BD,
∵ABCD是正方形,
∴AC⊥BD,
又PO?平面PAC,AC?平面PAC,PO∩AC=O,
∴BD⊥平面PAC,
又BD?平面BDE,
∴平面PAC⊥平面BDE.
点评 本题考查了线面平行,线面垂直的判定,面面垂直的判定,属于基础题.

练习册系列答案
相关题目
8.一个几何体的三视图如右图所示,其中俯视图是一个正三角形及其内切圆,则该几何体的体积为( )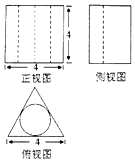

| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |
9.在△ABC中,角A,B,C所对的边分别为a,b,c,已知2a-b=2ccosB,则角C的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
13.已知函数$f(x)=\left\{{\begin{array}{l}{x+1,(x≤1)}\\{-x+1,(x>1)}\end{array}}\right.$,则f[f(2)]=( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
3. 我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
“今有蒲生一日,长三尺.莞生一日,长一尺.蒲生日自半.莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)
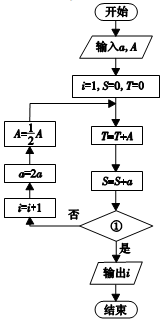
现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计右面的程序框图,输入A=3,a=1.那么在①处应填( )
 我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:“今有蒲生一日,长三尺.莞生一日,长一尺.蒲生日自半.莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)
现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计右面的程序框图,输入A=3,a=1.那么在①处应填( )
| A. | T>2S? | B. | S>2T? | C. | S<2T? | D. | T<2S? |
7.已知$\overrightarrow a$,$\overrightarrow b$为单位向量,其夹角为120°,则$(\overrightarrow a-2\overrightarrow b)•\overrightarrow b$=( )
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | -1 | D. | 2 |
5.甲、乙、丙、丁、戊5名学生各自在3门数学选修课:数学史、数学建模和几何画板中任选一门学习,则这三门课程都有同学选修且甲不选修几何画板的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{96}{125}$ | C. | $\frac{32}{81}$ | D. | $\frac{100}{243}$ |