某十字路口的信号灯为红灯和绿灯交替出现.红灯持续的时间为60秒.小明放学回家途经该路口遇到红灯.则小明至少要等15秒才能出现绿灯的概率为( )A．$\frac{2}{3}$B．$\frac{1}{3}$C．$\frac{3}{4}$D．$\frac{1}{4}$ 题目和参考答案——青夏教育精英家教网—

题目内容

20．某十字路口的信号灯为红灯和绿灯交替出现，红灯持续的时间为60秒，小明放学回家途经该路口遇到红灯，则小明至少要等15秒才能出现绿灯的概率为（　　）

A．

$\frac{2}{3}$

B．

$\frac{1}{3}$

C．

$\frac{3}{4}$

D．

$\frac{1}{4}$

分析求出一名行人前30秒来到该路口遇到红灯，即可求出至少需要等待20秒才出现绿灯的概率．

解答解：∵红灯持续时间为60秒，至少需要等待15秒才出现绿灯，
∴一名行人前45秒来到该路口遇到红灯，
∴至少需要等待15秒才出现绿灯的概率为$\frac{45}{60}$=$\frac{3}{4}$．
故选：C

点评本题考查概率的计算，考查古典概型，考查学生的计算能力，比较基础．

练习册系列答案

11．圆C₁：x²+y²+2ax+a²-9=0和圆C₂：x²+y²-4by-1+4b²=0只有一条公切线，若a∈R，b∈R，且ab≠0，则$\frac{4}{a^2}+\frac{1}{b^2}$的最小值为4．

8．一个几何体的三视图如右图所示，其中俯视图是一个正三角形及其内切圆，则该几何体的体积为（　　）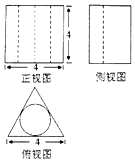

A．

$16\sqrt{3}-\frac{16π}{3}$

B．

$\frac{{16\sqrt{3}-16π}}{3}$

C．

$8\sqrt{3}-\frac{8π}{3}$

D．

$\frac{{8\sqrt{3}-8π}}{3}$

15．已知f（x）是定义在R上的函数，f'（x）是f（x）的导函数．给出如下四个结论：
①若$f'（x）+\frac{f（x）}{x}＞0$，且f（0）=e，则函数xf（x）有极小值0；
②若xf'（x）+2f（x）＞0，则4f（2ⁿ⁺¹）＜f（2ⁿ），n∈N^*；
③若f'（x）-f（x）＞0，则f（2017）＞ef（2016）；
④若f'（x）+f（x）＞0，且f（0）=1，则不等式f（x）＜e^-x的解集为（0，+∞）．
所有正确结论的序号是①③．

5．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左焦点F（-c，0）（c＞0）作圆${x^2}+{y^2}=\frac{a^2}{4}$的切线，切点为E，延长FE交双曲线右支于点P．若$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$，则双曲线的渐近线方程为（　　）

12．已知数列{a_n}的前n项和为S_n，点${P_n}（{n，{S_n}}）（{n∈{N^*}}）$是曲线f（x）=x²+2x上的点．数列{a_n}是等比数列，且满足b₁=a₁，b₂=a₄．
（1）求数列{a_n}，{b_n}的通项公式；
（2）记${c_n}={（{-1}）^n}{a_n}+{b_n}$，求数列{c_n}的前n项和T_n．

9．在△ABC中，角A，B，C所对的边分别为a，b，c，已知2a-b=2ccosB，则角C的大小为（　　）

10．?x₀∈（2，+∞），k（x₀-2）＞x₀（lnx₀+1），则正整数k的最小值为5．
（参考数据：ln2≈0.6931，ln3≈1.0986，ln5≈1.6094）

试题分类