题目内容
18.一个三棱锥的三视图如图所示,则其外接球的体积是$\frac{125\sqrt{2}}{3}π$.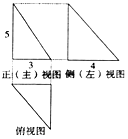
分析 由已知中几何体的三视图,画出几何体的直观图,进而求出几何体的外接球的半径,可得答案.
解答 解:观察三视图,可得直观图如图所示.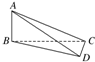
该三棱锥ABCD的底面BCD是直角三角形,
AB⊥平面BCD,CD⊥BC,
侧面ABC,ABD是直角三角形;
由CD⊥BC,CD⊥AB,知CD⊥平面ABC,CD⊥AC,
AD是三棱锥ABCD外接球的直径,
AD2=AB2+BC2+CD2=50,
所以AD=5$\sqrt{2}$,
三棱锥ABCD外接球的体积V=$\frac{4}{3}π•(\frac{5\sqrt{2}}{2})^{3}$=$\frac{125\sqrt{2}}{3}π$,
故答案为$\frac{125\sqrt{2}}{3}π$.
点评 本题考查的知识点是球的内接多面体,球的体积和表面积,棱锥的三视图,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)$,过x轴上点P的直线l与双曲线的右支交于M,N两点(M在第一象限),直线MO交双曲线左支于点Q(O为坐标原点),连接QN.若∠MPO=60°,∠MNQ=30°,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
7.(2-i)(-2+i)=( )
| A. | -5 | B. | -3+4i | C. | -3 | D. | -5+4i |
8.一个几何体的三视图如右图所示,其中俯视图是一个正三角形及其内切圆,则该几何体的体积为( )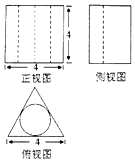

| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |