题目内容
3.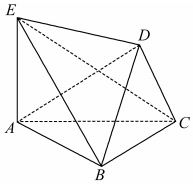 如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.
如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.(Ⅰ)求证:AE∥面DBC;
(Ⅱ)若AB⊥BC,BD⊥CD,求证:面ADB⊥面EDC.
分析 (I)过点D作DO⊥BC,O为垂足,则由面面垂直的性质得出DO⊥平面ABC,于是AE∥DO,从而得出AE∥面DBC;
(II)由面面垂直的性质可得AB⊥平面BCD,故AB⊥CD,结合BD⊥CD可得CD⊥平面ABD,从而得出面ADB⊥面EDC.
解答 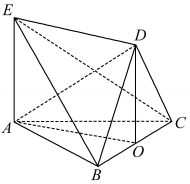 证明:(Ⅰ)过点D作DO⊥BC,O为垂足,
证明:(Ⅰ)过点D作DO⊥BC,O为垂足,
∵面DBC⊥面ABC,面DBC∩面ABC=BC,DO?面DBC,
∴DO⊥面ABC,
又AE⊥面ABC,
∴AE∥DO,
又AE?面DBC,DO?面DBC,
∴AE∥面DBC.
(Ⅱ)∵面DBC⊥面ABC,面DBC∩面ABC=BC,AB⊥BC,
∴AB⊥面DBC,
又DC?面DBC,
∴AB⊥DC,
又BD⊥CD,AB∩BD=B,AB、BD?面ADB,
∴DC⊥面ADB,
又DC?面EDC,
∴面ADB⊥面EDC.
点评 本题考查了面面垂直的性质与判定,线面垂直的性质,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
14.函数f(x)=6cos($\frac{3π}{2}$+x)-cos2x的最小值是( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
18.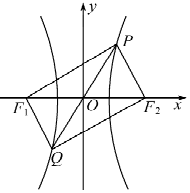 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
8.一个几何体的三视图如右图所示,其中俯视图是一个正三角形及其内切圆,则该几何体的体积为( )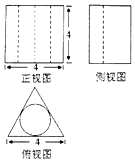

| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |