题目内容
19.设函数f(x)=sin(ωx+φ)(φ>0)的图象关于直线x=-1和x=2对称,则f(0)的取值集合是( )| A. | {-1,1,-$\frac{1}{2}$} | B. | {1,-$\frac{1}{2}$,$\frac{1}{2}$} | C. | {-1,1,-$\frac{1}{2}$,$\frac{1}{2}$} | D. | {-1,1,-2,2} |
分析 由题意图象关于直线x=-1和x=2对称,可得周期T=6或T=3.对其讨论.可得答案.
解答 解:函数f(x)=sin(ωx+φ)(φ>0)的图象关于直线x=-1和x=2对称,
ωx+φ=$\frac{π}{2}+kπ$,(k∈Z)
当x=0时,φ=$\frac{π}{2}+kπ$,
那么:f(0)=sinφ=±1.
当直线x=-1和x=2是相邻对称轴,那么:周期T=6.函数f(x)=sin($\frac{1}{3}$πx+φ)
若x=-1过图象最低点时,则x=2过图象最高点,那么φ=$\frac{11π}{6}$.
若x=-1过图象最高点时,则x=2过图象最低点,那么φ=$\frac{5π}{6}$
∴f(0)=sinφ=$\frac{1}{2}$或$-\frac{1}{2}$.
则f(0)的取值集合为{±1,$±\frac{1}{2}$}.
故选:C.
点评 本题主要考查了对称的问题和周期的讨论.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.(2-i)(-2+i)=( )
| A. | -5 | B. | -3+4i | C. | -3 | D. | -5+4i |
14.函数f(x)=6cos($\frac{3π}{2}$+x)-cos2x的最小值是( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
4.设集合A={x|x2-2x-3<0},B={x|y=ln(2-x)},则A∩B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x<2} | C. | {x|-3<x<2} | D. | {x|1<x<2} |
8.一个几何体的三视图如右图所示,其中俯视图是一个正三角形及其内切圆,则该几何体的体积为( )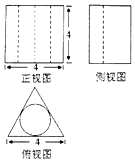

| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |
9.在△ABC中,角A,B,C所对的边分别为a,b,c,已知2a-b=2ccosB,则角C的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |