题目内容
设函数f(x)=cos(2x-
)+2sin(x+
)sin(x-
)
(1)求函数f(x)的最小正周期和单调减区间;
(2)若函数f(x)-m=0在区间[0,
]上有两个零点,求m的取值范围.
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
(1)求函数f(x)的最小正周期和单调减区间;
(2)若函数f(x)-m=0在区间[0,
| 2π |
| 3 |
考点:两角和与差的正弦函数,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)利用两角和公式和诱导公式及倍角公式对函数解析式化简整理得关于x的正弦函数,利用三角函数的性质可取的函数的最小正周期和单调区间.
(2)要使若函数f(x)-m=0在区间[0,
]上有两个零点,即y=f(x)和y=m的图象在此范围有两个交点,分别画出两函数的图象,利用图象可直观得到答案.
(2)要使若函数f(x)-m=0在区间[0,
| 2π |
| 3 |
解答:
解:(1)f(x)=cos(2x-
)+2sin(x+
)sin(x-
)
=cos2x•
+sin2x•
-2sin(x+
)cos(x+
)
=cos2x•
+sin2x•
-sin(2x+
)
=cos2x•
+sin2x•
-sin2x
=
sin2x-
cos2x
=sin(2x-
).
∴T=
=π,
当2kπ+
≤2x-
≤2kπ+
,即kπ+
≤x≤
+kπ时,k∈Z,函数单调减,
∴函数的单调递减区间为[kπ+
,
+kπ](k∈Z).
(2)根据五点画图法,可求得
故其图象为:
函数f(x)-m=0在区间[0,
]上有两个零点,需y=f(x)和y=m的图象有两个交点,
如图当0<m≤1时,-
≤m<0时,直线与正弦函数图象有两个交点.
故m的范围[-
,0)∪(0,1].
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
=cos2x•
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
=cos2x•
| 1 |
| 2 |
| ||
| 2 |
| π |
| 2 |
=cos2x•
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
∴T=
| 2π |
| 2 |
当2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| 2π |
| 3 |
| 5π |
| 3 |
∴函数的单调递减区间为[kπ+
| 2π |
| 3 |
| 5π |
| 3 |
(2)根据五点画图法,可求得

故其图象为:

函数f(x)-m=0在区间[0,
| 2π |
| 3 |
如图当0<m≤1时,-
| 1 |
| 2 |
故m的范围[-
| 1 |
| 2 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.利用数形结合的思想较为直观.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数z=
+2i的模为( )
| 5-3i |
| 1-i |
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、4
|
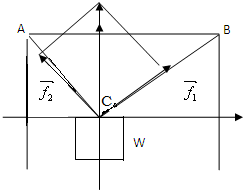 物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.
物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.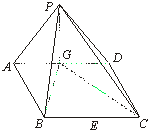 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.