题目内容
已知函数f(x)=sinx,对于满足0<x1<x2<π的任意x1,x2,给出下列结论:
①(x2-x1)[f(x2)-f(x1)]>0
②x2f(x1)>x1f(x2)
③f(x2)-f(x1)<x2-x1
④
<f(
)
其中正确结论的序号为 .(把所有正确结论的序号填上)
①(x2-x1)[f(x2)-f(x1)]>0
②x2f(x1)>x1f(x2)
③f(x2)-f(x1)<x2-x1
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
其中正确结论的序号为
考点:正弦函数的单调性
专题:函数的性质及应用
分析:根据正弦函数的图象结合函数的性质分别进行判断即可得到结论.
解答:
解:①由(x2-x1)[f(x2)-f(x1)]>0可知函数f(x)为增函数,∵f(x)=sinx,在0<x<π上不单调,∴①错误.
②由x2f(x1)>x1f(x2)得
>
,即前一点的斜率大于后一点的斜率,由图象知正确.
③由f(x2)-f(x1)<x2-x1,得
<1,即对于割线斜率小于1,f′(x)=cosx<1,∴③正确.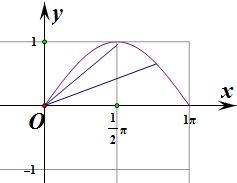
④由
<f(
)可知函数为凸函数,∴④正确.
故答案为:②③④
②由x2f(x1)>x1f(x2)得
| f(x1) |
| x1 |
| f(x2) |
| x2 |
③由f(x2)-f(x1)<x2-x1,得
| f(x2)-f(x1) |
| x2-x1 |

④由
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
故答案为:②③④
点评:本题主要考查三角函数的图象和性质,利用函数的单调性,斜率以及凸凹性是解决本题的关键.

练习册系列答案
相关题目
设函数f(x)=cos(2x-
)+2sin(x+
)sin(x-
)
(1)求函数f(x)的最小正周期和单调减区间;
(2)若函数f(x)-m=0在区间[0,
]上有两个零点,求m的取值范围.
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
(1)求函数f(x)的最小正周期和单调减区间;
(2)若函数f(x)-m=0在区间[0,
| 2π |
| 3 |
某地区气象台统计,该地区下雨的概率是
,刮风的概率为
,既刮风又下雨的概率为
,则在下雨天里,刮风的概率为( )
| 4 |
| 15 |
| 2 |
| 15 |
| 1 |
| 10 |
A、
| ||
B、
| ||
C、
| ||
D、
|