题目内容
已知向量
=(-cosx,sinx),
=(cosx,cosx),设f(x)=
•
+1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间.
| a |
| b |
| a |
| b |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间.
考点:三角函数中的恒等变换应用,平面向量数量积的运算,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)根据平面向量的数量积的坐标运算,并结合二倍角公式和辅助角公式,得到f(x)=
sin(2x-
)-
,然后,借助于周期公式进行求解;
(2)直接结合三角函数的单调性进行求解即可.
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
(2)直接结合三角函数的单调性进行求解即可.
解答:
解:(1)∵
=(-cosx,sinx),
=(cosx,cosx),
∴f(x)=
•
+1
=sinxcosx-cos2x
=
sin(2x-
)-
,
∴f(x)=
sin(2x-
)-
,
∴T=
=π,
∴函数f(x)的最小正周期π;
(2)∵f(x)=
sin(2x-
)-
,
∴
+2kπ≤2x-
≤
+2kπ,k∈Z,
∴
+kπ≤x≤
+kπ,
∴函数f(x)的单调减区间[
+kπ,
+kπ],(k∈Z).
| a |
| b |
∴f(x)=
| a |
| b |
=sinxcosx-cos2x
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴f(x)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴T=
| 2π |
| 2 |
∴函数f(x)的最小正周期π;
(2)∵f(x)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
∴
| 3π |
| 8 |
| 7π |
| 8 |
∴函数f(x)的单调减区间[
| 3π |
| 8 |
| 7π |
| 8 |
点评:本题重点考查了三角函数的图象与性质、三角恒等变换等公式、辅助角公式等知识,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
曲线f(x)=x3+x-2的一条切线平行于直线y=4x-1,则切点P0的坐标为( )
| A、(0,-1)或(1,0) |
| B、(1,0)或(-1,-4) |
| C、(-1,-4)或(0,-2) |
| D、(1,0)或(2,8) |
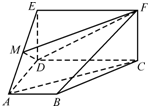 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=