题目内容
已知二次函数f(x)=ax2+bx(a≠0,a、b为常数)满足f(1-x)=f(1+x),且方程f(x)=x有两相等实根.
(1)在区间x∈[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
(2)是否存在实数m和n(m<n ),使f(x)的定义域和值域分别为[m,n]和[3m,3n],如果存在求出m和n的值.
(1)在区间x∈[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
(2)是否存在实数m和n(m<n ),使f(x)的定义域和值域分别为[m,n]和[3m,3n],如果存在求出m和n的值.
考点:导数在最大值、最小值问题中的应用,函数的定义域及其求法,函数的值域,函数的零点
专题:导数的综合应用
分析:(1)由f(1-x)=f(1+x),得函数的对称轴为x=1,又方程f(x)=x有两相等实根,即ax2+(b-1)x=0有两相等实根,利用△=0可得关于a,b的方程,由此可求出a,b的值.区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,转化成二次函数在区间[-1,1]上恒为正,借助二次函数的性质转化即可求参数.
(2)借助函数的单调性确定出函数在[m,n]上的单调性,找到区间中那个自变量的函数值是3m,3n,由此建立方程求解,若能解出值,说明存在,否则不存在.
(2)借助函数的单调性确定出函数在[m,n]上的单调性,找到区间中那个自变量的函数值是3m,3n,由此建立方程求解,若能解出值,说明存在,否则不存在.
解答:
解:(1)∵f(1-x)=f(1+x),∴f(x)的对称轴为x=1,
即-
=1
即b=-2a.
∵f(x)=x有两相等实根,∴ax2+bx=x,
即ax2+(b-1)x=0有等根0,
∴b=1,a=-
∴f(x)=-
x2+x
在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,
即-
x2+x>2x+m在区间[-1,1]上恒成立
即x2+2x+2m<0在区间[-1,1]上恒成立
故有
,
解得m<-
,
∴当m<-
时,在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方.
(2)f(x)=-
x2+x=-
(x-1)2+
≤
故3n≤
,故m<n≤
又函数的对称轴为x=1,故f(x)在[m,n]单调递增
则有
解得
或
,
又m<n,
∴m=-4,n=0.
即-
| b |
| 2a |
即b=-2a.
∵f(x)=x有两相等实根,∴ax2+bx=x,
即ax2+(b-1)x=0有等根0,
∴b=1,a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,
即-
| 1 |
| 2 |
即x2+2x+2m<0在区间[-1,1]上恒成立
故有
|
解得m<-
| 3 |
| 2 |
∴当m<-
| 3 |
| 2 |
(2)f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故3n≤
| 1 |
| 2 |
| 1 |
| 6 |
又函数的对称轴为x=1,故f(x)在[m,n]单调递增
则有
|
解得
|
|
又m<n,
∴m=-4,n=0.
点评:本题考点是二次函数的性质考查综合利用函数的性质与图象转化解题,属于难题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知函数y=f(x)是定义在R上的奇函数,且当x>0时,f(x)+xf′(x)>0.(其中f′(x)是f(x)的导函数).设a=(log
4)•f(log
4),b=
•f(
).c=(lg
)•f(lg
),判断大小为( )
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| A、c>a>b |
| B、a>b>c |
| C、c>b>a |
| D、a>c>b |

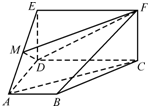 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=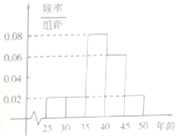 2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.
2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.