Question

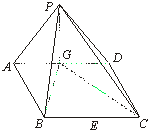如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，且∠DAB=60°．侧面PAD为正三角形，其所在的平面垂直于底面ABCD，G为AD边的中点．
（1）求证：BG⊥平面PAD；
（2）求三棱锥G-CDP的体积；
（3）若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD，并证明你的结论．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的判定,平面与平面垂直的判定

专题：空间位置关系与距离

分析：（1）首先，证明△ABD为正三角形，然后，根据三角形的性质，得到BG⊥AD，最后，根据平面PAD⊥平面ABCD，得到BG⊥平面PAD；
（2）先证明PG⊥平面ABCD，然后，求解PG的长，最后，利用椎体的体积公式进行求解；
（3）先写出结论：当F为PC的中点时，平面DEF⊥平面ABCD，然后，结合取中点，构造平行四边形，证明FH⊥平面ABCD，最后，利用面面垂直的判定定理得证．

解答： 解：（1）证明：连结BD．
∵ABCD为棱形，且∠DAB=60°，
∴△ABD为正三角形．
又G为AD的中点，
∴BG⊥AD．
又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，
∴BG⊥平面PAD．
（2）∵G为正三角形PAD的边AD的中点，
∴PG⊥AD．
又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，
∴PG⊥平面ABCD．
∵正三角形PAD的边长为2，
∴PG=

3

．
在△CDG中，CD=2，DG=1，∠CDG=120°，
∴S△CDG=

1

2

×1×2×

3

2

=

3

2

．
故VG-CDP=VP-CDG=

1

3

×

3

×

3

2

=

1

2

．
（3）当F为PC的中点时，平面DEF⊥平面ABCD．
取PC的中点F，连结DE，EF，DF，CG，且DE与CG相交于H．
∵E、G分别为BC、AD的中点，
∴四边形CDGE为平行四边形．
故H为CG的中点．又F为CP的中点，
∴FH∥PG．
由（2），得PG⊥平面ABCD，
∴FH⊥平面ABCD．
又FH?平面DEF，
∴平面DEF⊥平面ABCD．

点评：本题综合考查了空间中：线线平行、线面垂直、面面垂直等定理的应用，三角形的有关性质及其应用，本题中多次出现了中点问题，这在高考中经常出现，处理中点问题的方法口诀为：有中点，连中点，立马得到中位线；无中点，取中点，相连得到中位线．