题目内容
直线m在平面α内,直线n在平面β内,下列命题正确的是( )
| A、m⊥n⇒α⊥β |
| B、α∥β⇒m∥β |
| C、m⊥n⇒m⊥β |
| D、m∥n⇒α∥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:由m?α,n?β,结合面面垂直的判定方法和面面平行的判定方法,逐一判断四个答案的正误,可得结论.
解答:
解:∵m?α,n?β,若m⊥n,则α与β可能平行也可能相交,故A错误;
若α∥β,根据面面平行的定义,可知两个平面没有公共点,由m?α可知,m与β没有公共点,即m∥β,故B正确;
若m⊥n,则m与β可能平行,也可能相交,故C错误;
若m∥n,则α与β可能平行也可能相交,故D错误;
故选:B
若α∥β,根据面面平行的定义,可知两个平面没有公共点,由m?α可知,m与β没有公共点,即m∥β,故B正确;
若m⊥n,则m与β可能平行,也可能相交,故C错误;
若m∥n,则α与β可能平行也可能相交,故D错误;
故选:B
点评:本题考查的知识点是空间直线与平面之间的位置关系,熟练掌握空间线面关系,面面关系,线线关系的定义,几何特征及性质和判定方法是解答的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知实数x,y满足不等式组
,则目标函数z=3x-4y的最小值m与最大值M的积为( )
|
| A、-60 | B、-48 |
| C、-80 | D、36 |
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥n,m⊥α,则n⊥α |
| C、若m∥α,m∥β,则α∥β |
| D、若m∥α,α⊥β,则m⊥β |
如果loga8>logb8>0,那么a、b间的关系是( )
| A、0<a<b<1 |
| B、1<a<b |
| C、0<b<a<1 |
| D、1<b<a |
设m、n是两条不同的直线,α、β是两个不同的平面.下列四个命题中,正确的是( )
| A、α∥β,m?α,n?β,则m∥n |
| B、α⊥β,m⊥β,则m∥α或m?α |
| C、α⊥β,m?α,n?β,则m⊥n |
| D、α∥β,m⊥β,n⊥α,则m∥n |
设正项等比数列{an}的前n项和为Sn,公比为q,若Sk-2=3,Sk=15,Sk+2=63,则q=( )
| A、-2 | B、2 | C、-4 | D、4 |
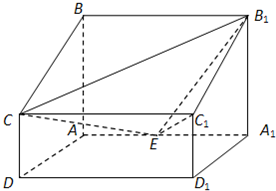 四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为AA1的中点.
四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为AA1的中点.