题目内容
已知函数f(x)=e|x|+x2(e为自然对数的底数),且f(3a-2)>f(a-1),则实数a的取值范围为 .
考点:指数函数综合题
专题:函数的性质及应用
分析:根据函数式子得出f(-x)=f(x)=f(|x|),且在(0,+∞)单调递增,把f(3a-2)>f(a-1),转化为|3a-2|>|a-1|,即8a2-10a+3>0,求解即得到实数a的取值范围.
解答:
解:∵函数f(x)=e|x|+x2(e为自然对数的底数),
∴f(-x)=f(x)=f(|x|),且在(0,+∞)单调递增,
∵f(3a-2)>f(a-1),
∴|3a-2|>|a-1|,
即8a2-10a+3>0,
实数a的取值范围为a<
或a>
,
故答案为:(-∞,
)∪(
,+∞)
∴f(-x)=f(x)=f(|x|),且在(0,+∞)单调递增,
∵f(3a-2)>f(a-1),
∴|3a-2|>|a-1|,
即8a2-10a+3>0,
实数a的取值范围为a<
| 1 |
| 2 |
| 3 |
| 4 |
故答案为:(-∞,
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题考察了偶函数的性质,单调性,求解不等式,属于中档题.

练习册系列答案
相关题目
函数f(x)=x2+(2a2-6a)x+2在区间(-∞,2]上单调递减,那么实数a的取值范围( )
| A、[1,+∞) |
| B、(-∞,2] |
| C、[1,2] |
| D、(-∞,1]∪[2,+∞) |
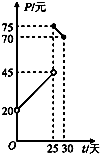 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表: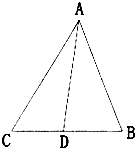 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2