题目内容
若函数:s=
<0,则函数在t=1的切线方程为 .
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求导数,可得函数在x=1处的导数,也就是切线的斜率,再利用点斜式求出切线方程即可.
解答:
解:由题意,s=3t2+2,∴s′=6t,
∴t=1时,s′=6,s=5,
∴函数在t=1的切线方程为y-5=6(x-1),即y=6x-1.
故答案为:y=6x-1.
∴t=1时,s′=6,s=5,
∴函数在t=1的切线方程为y-5=6(x-1),即y=6x-1.
故答案为:y=6x-1.
点评:本题考查了利用导数研究在曲线某点处的切线方程,以及导数的几何意义,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列几个图形中,可以表示函数关系y=f(x)的一个图是( )
A、 |
B、 |
C、 |
D、 |
设f(x)=x3+log2(x+
),若a,b∈R,且 f(a)+f(b)≥0,则一定有( )
| x2+1 |
| A、a+b≤0 |
| B、a+b<0 |
| C、a+b≥0 |
| D、a+b>0 |
已知函数f(x)=-x+log2
+1,则f(
)+f(-
)的值为( )
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、2log2
|
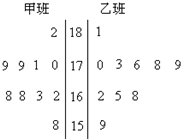 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图