题目内容
已知点P是圆C:x2+y2-4ax-2by-5=0(a>0,b>0)上任意一点,若点P关于直线x+2y-1=0的对称点仍在圆C上,则
+
的最小值是 .
| 4 |
| a |
| 1 |
| b |
考点:圆的一般方程
专题:计算题,不等式的解法及应用,直线与圆
分析:由题意,x2+y2-4ax-2by-5=0表示的是以(2a,b)为圆心的圆,则直线x+2y-1=0过圆心,从而可得a+b=
(a>0,b>0),利用不等式即可.
| 1 |
| 2 |
解答:
解:x2+y2-4ax-2by-5=0表示的是以(2a,b)为圆心的圆,
故由曲线x2+y2-4ax-2by-5=0上的任意一点关于直线x+2y-1=0的对称点仍在圆C上可得,
直线x+2y-1=0过点(2a,b),则2a+2b-1=0,
即a+b=
(a>0,b>0),
则
+
=2(a+b)(
+
)=2(5+
+
)≥2(5+4)=18.(当且仅当
=
时,等号成立)
故答案为:18.
故由曲线x2+y2-4ax-2by-5=0上的任意一点关于直线x+2y-1=0的对称点仍在圆C上可得,
直线x+2y-1=0过点(2a,b),则2a+2b-1=0,
即a+b=
| 1 |
| 2 |
则
| 4 |
| a |
| 1 |
| b |
| 4 |
| a |
| 1 |
| b |
| a |
| b |
| 4b |
| a |
| a |
| b |
| 4b |
| a |
故答案为:18.
点评:本题考查了恒成立问题及圆的结构特征,同时考查了基本不等式的应用,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
x,y满足约束条件
,若z=y-2ax取得最大值的最优解不唯一,则实数a的值为( )
|
A、
| ||
B、1或-
| ||
| C、2或1 | ||
| D、2或-1 |
下列判断正确的是( )
| A、1.50.3>0.80.3 | ||||||
| B、1.52.5>1.53 | ||||||
| C、0.83<0.84 | ||||||
D、(
|
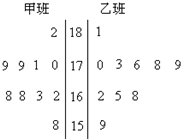 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图