题目内容
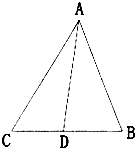 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2| A-B |
| 2 |
| 1 |
| 7 |
考点:解三角形
专题:计算题,解三角形
分析:利用二倍角公式,和角的余弦公式,可求C,利用正弦定理、余弦定理求出边AB的长.
解答:
解:∵4sin2
+4sinAsinB=3,
∴2[1-cos(A-B)+4sinAsinB=3,
∴2-2(cosAcosB+sinAsinB)+4sinAsinB=3,
∴cos(A+B)=-
,
∴cosC=
,
∴C=
.
∵cos∠ADB=
,
∴cos∠ADC=-
,
∴sin∠ADC=
,
在△ADC中,由正弦定理可得AD=
•sinC=7
∴AB=
=7.
| A-B |
| 2 |
∴2[1-cos(A-B)+4sinAsinB=3,
∴2-2(cosAcosB+sinAsinB)+4sinAsinB=3,
∴cos(A+B)=-
| 1 |
| 2 |
∴cosC=
| 1 |
| 2 |
∴C=
| π |
| 3 |
∵cos∠ADB=
| 1 |
| 7 |
∴cos∠ADC=-
| 1 |
| 7 |
∴sin∠ADC=
4
| ||
| 7 |
在△ADC中,由正弦定理可得AD=
| AC |
| sin∠ADC |
∴AB=
49+4-2×7×2×
|
点评:本题考查二倍角公式,和角的余弦公式,考查正弦定理、余弦定理,属于中档题.

练习册系列答案
相关题目
设f(x)=x3+log2(x+
),若a,b∈R,且 f(a)+f(b)≥0,则一定有( )
| x2+1 |
| A、a+b≤0 |
| B、a+b<0 |
| C、a+b≥0 |
| D、a+b>0 |
已知函数f(x)=-x+log2
+1,则f(
)+f(-
)的值为( )
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、2log2
|
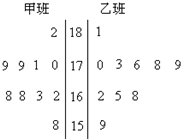 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图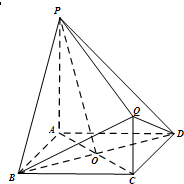 如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O
如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O