Question

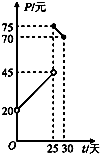某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图表示，该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表：

t/天	5	10	20	30
Q/件	45	40	30	20

（Ⅰ）根据提供的图象（如图），写出该商品每件的销售价格P与时间t的函数关系式；
（Ⅱ）根据表1提供的数据，写出日销售量Q与时间t的一次函数关系式；
（Ⅲ）求该商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天．（日销售金额=每件的销售价格×日销售量）．

Answer 1

考点：根据实际问题选择函数类型

专题：应用题,函数的性质及应用

分析：（I）由已知中的函数图象，利用待定系数法，分别求出两段函数图象对应的解析式，进而可得该商品每件的销售价格P与时间t的函数关系；
（Ⅱ）根据表中提供的数据，利用待定系数法，可得日销售量Q与时间t的一个函数关系式；
（Ⅲ）根据分段函数不同段上的表达式，分别求最大值最终取较大者分析即可获得问题解答．

解答： 解：（I）根据图象甲，当0＜t＜25时，P=t+20，当25≤t≤30时，P=-t+100，…（2分）
∴每件商品的销售价格P与时间t的函数关系式
P=

t+20，0＜t＜25 -t+100，25≤t≤30

（t∈N）…（4分）
（II）可设日销售量Q与时间t的一次函数关系式为Q=kt+b，将（10，40），（20，30）代入易求得k=-1，b=50，
∴日销售量Q与时间t的一个函数关系式为Q=-t+50（0＜t≤30，t∈N）．               …（7分）
（III）当0＜t＜25，t∈N₊时，y=（t+20）（-t+50）=-t²+30t+1000=-（t-15）²+775．
∴t=15（天）时，y_max=775（元），
当25≤t≤30，t∈N₊时，y=（-t+100）（-t+50）=t²-150t+5000=（t-75）²-225，在t∈[25，30]时，函数递减．∴t=25（天）时，y_max=1875（元）．
∵1875＞775，∴y_max=1875（元）．
故所求日销售金额的最大值为1125元，且在最近30天中的第25天日销售额最大．…（13分）

点评：本题考查的知识点是函数模型的选择与应用，熟练掌握待定系数法求函数解析式及二次函数的图象和性质是解答的关键．