题目内容
已知函数f(x)=-
x2+xsinx+cosx,x∈[-π,π].
(1)判断函数y=f(x)奇偶性,并求其单调区间;
(2)若曲线y=f(x)与直线y=b有两个交点,求b的取值范围.
| 1 |
| 4 |
(1)判断函数y=f(x)奇偶性,并求其单调区间;
(2)若曲线y=f(x)与直线y=b有两个交点,求b的取值范围.
考点:函数奇偶性的判断,函数的图象
专题:函数的性质及应用
分析:(1)利用函数的奇偶性的定义判断f(-x)与f(x)的关系;利用偶函数的形状以及求导求函数的单调区间;
(2)利用(1)求的单调区间画出函数图象,利用数形结合求满足条件的b的范围.
(2)利用(1)求的单调区间画出函数图象,利用数形结合求满足条件的b的范围.
解答:
解:(1)由已知,函数的定义域定义原点对称,并且f(-x)=-
x2-xsin(-x)+cos(-x)=-
x2+xsinx+cosx=f(x),所以函数f(x)是偶函数;
当x∈[0,π]时,f′(x)=-
x+sinx+xcosx-sinx=x(cosx-
);f′(x)>0时,cosx>
,x∈(0,
);
f′(x)<0时,cosx<
,x∈(
,π);
又f(x)为偶函数,所以f(x)的递增期间为[-π,-
],[0,
];
递减区间为:(-
,0),(
,π);
(2)由(1)画出函数图象如图
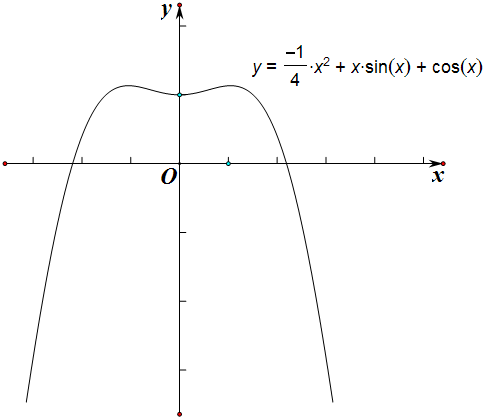
曲线y=f(x)与直线y=b有两个交点,f(π)≤b≤f(0)或者b=f(
)时有两个交点,
所以-
≤b<1或b=-
+
+
时曲线y=f(x)与直线y=b有两个交点.
| 1 |
| 4 |
| 1 |
| 4 |
当x∈[0,π]时,f′(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
f′(x)<0时,cosx<
| 1 |
| 2 |
| π |
| 3 |
又f(x)为偶函数,所以f(x)的递增期间为[-π,-
| π |
| 3 |
| π |
| 3 |
递减区间为:(-
| π |
| 3 |
| π |
| 3 |
(2)由(1)画出函数图象如图
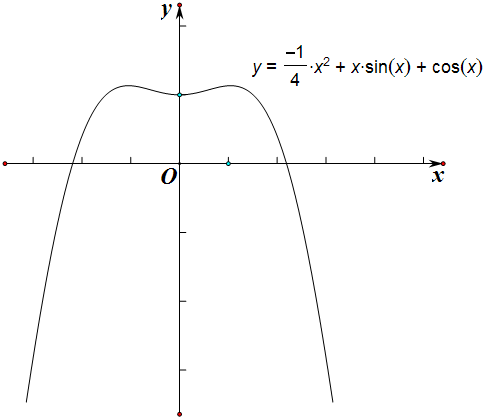
曲线y=f(x)与直线y=b有两个交点,f(π)≤b≤f(0)或者b=f(
| π |
| 3 |
所以-
| π2 |
| 4 |
| π2 |
| 36 |
| ||
| 6 |
| 1 |
| 2 |
点评:本题考查了函数奇偶性的判断以及利用导数求函数的单调区间以及最值的方法;数形结合是解答本题的技巧,注意体会.

练习册系列答案
相关题目
下列判断正确的是( )
A、函数f(x)=
| ||||
B、函数f(x)=(1-x)
| ||||
C、函数f(x)=
| ||||
| D、函数f(x)=1既是奇函数又是偶函数 |
已知函数f(x)=
,若f(x)=10,则x=( )
|
| A、3 | B、-3 |
| C、-5或-3 | D、-5或-3或3 |
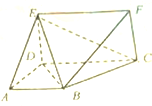 如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.
如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.