题目内容
已知函数y=f(x),(x≠0)对于任意的x,y∈R且x,y≠0满足f(xy)=f(x)+f(y).
(Ⅰ)求f(1),f(-1)的值;
(Ⅱ)判断函数y=f(x),(x≠0)的奇偶性;
(Ⅲ)若函数y=f(x)在(0,+∞)上是增函数,解不等式f(
x)+f(x-5)≤0.
(Ⅰ)求f(1),f(-1)的值;
(Ⅱ)判断函数y=f(x),(x≠0)的奇偶性;
(Ⅲ)若函数y=f(x)在(0,+∞)上是增函数,解不等式f(
| 1 |
| 6 |
考点:函数单调性的性质,函数奇偶性的判断
专题:函数的性质及应用
分析:(Ⅰ)赋值法:在所给等式中,令x=y=1,可求得f(1),令x=y=-1可求得f(-1);
(Ⅱ)在所给等式中令y=-1,可得f(-x)与f(x)的关系,利用奇偶性的定义即可判断;
(3)由题意不等式f(
x)+f(x-5)≤0可化为f(|
x(x-5)|)≤f(1),根据单调性即可去掉符号“f”,转化为具体不等式即可解得.
(Ⅱ)在所给等式中令y=-1,可得f(-x)与f(x)的关系,利用奇偶性的定义即可判断;
(3)由题意不等式f(
| 1 |
| 6 |
| 1 |
| 6 |
解答:
解:(Ⅰ)∵对于任意的x,y∈R且x,y≠0满足f(xy)=f(x)+f(y),
∴令x=y=1,得到:f(1)=f(1)+f(1),
∴f(1)=0,
令x=y=-1,得到:f(1)=f(-1)+f(-1),
∴f(-1)=0;
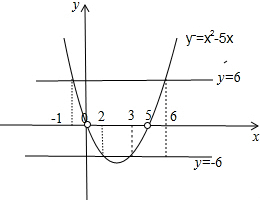
证明:(Ⅱ)由题意可知,令y=-1,得f(-x)=f(x)+f(-1),
∵f(-1)=0,∴f(-x)=f(x),
∴y=f(x)为偶函数;
解:(Ⅲ)由(Ⅱ)函数f(x)是定义在非零实数集上的偶函数.
∴不等式f(
x)+f(x-5)≤0可化为f[
x(x-5)]≤f(1),f(|
x(x-5)|)≤f(1),
∴-1≤
x(x-5)≤1,即:-6≤x(x-5)≤6且x≠0,x-5≠0,
在坐标系内,如图函数y=x(x-5)图象与y=6,y=-6两直线.
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6],
故不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6].
∴令x=y=1,得到:f(1)=f(1)+f(1),
∴f(1)=0,
令x=y=-1,得到:f(1)=f(-1)+f(-1),
∴f(-1)=0;
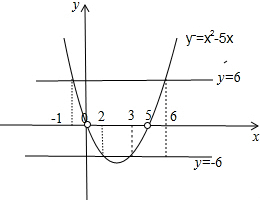
证明:(Ⅱ)由题意可知,令y=-1,得f(-x)=f(x)+f(-1),
∵f(-1)=0,∴f(-x)=f(x),
∴y=f(x)为偶函数;
解:(Ⅲ)由(Ⅱ)函数f(x)是定义在非零实数集上的偶函数.
∴不等式f(
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
∴-1≤
| 1 |
| 6 |
在坐标系内,如图函数y=x(x-5)图象与y=6,y=-6两直线.
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6],
故不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6].
点评:本题考查抽象函数的求值、奇偶性的判断及抽象不等式的解法,定义是解决抽象函数问题的常用方法,解抽象不等式关键是利用函数性质转化为具体不等式.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
若a=3tan60°,b=log
cos60°,c=log2tan30°,则( )
| 1 |
| 3 |
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、b>a>c |
6.若s1=∫
cosxdx,s2=∫
dx,s3=∫
exdx 则s1,s2,s3的大小关系是( )
| ||
| 0 |
| ||
| 1 |
| 1 |
| x |
| ||
| 1 |
| A、s2<s1<s3 |
| B、s1<s2<s3 |
| C、s2<s3<s1 |
| D、s3<s2<s1 |